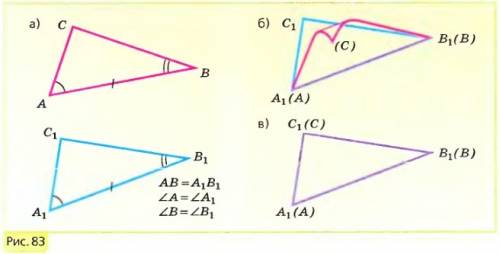
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых AB = A1B1, ∠A = ∠A1, ∠B = ∠B1 (рис. 83, а), и докажем, что эти треугольники равны.
Мысленно наложим треугольник ABC так, чтобы вершина A совместилась с вершиной A1, сторона AB – с равной ей стороной A1B1, а вершина C и C1 оказались по одну сторону от прямой A1B1 (рис. 83, б).
Так как ∠A = ∠A1 и ∠B = ∠B1, то сторона AC наложится на луч A1C1, а сторона BC – на луч B1C1. Поэтому вершина C – общая точка сторон AC и BC – совместится с общей точкой лучей A1C1 и B1C1, т. е. с точкой C1 (рис. 83, в). Из этого следует, что стороны AC и BC совместятся соответственно со сторонами A1C1 и B1C1. Итак, треугольники полностью совместятся, и, следовательно, они равны. Теорема доказана.
AOD - прямоугольный треугольник.
ОР - высота из прямого угла в треугольнике AOD.
ОР=√(АР*РD)=√(6√3*2√3)=6см.
По Пифагору АО=√(АР²+ОР²)=√(108+36)=12см.
R=AJ=JO=JP = АО/2 = 6см.
Площадь круга Sк=π*R²=36π.
В прямоугольном треугольнике АРО катет ОР равен половине
гипотенузы АО, значит <PAO=30°,
<РАК=60° (так как АО - биссектриса <PAK) => дуга РОК=120°.
<PJK=120°(центральный угол, опирающийся на дугу РОК).
РН=0,5*АР=3√3см (катет против угла 30°).
AH=√(АР²-РH²)=√(108-27)=9см.
Площадь треугольника АКР равна
Sapk=AH*PH=9*3√3=27√3см².
Площадь сегмента КОР равна
Skop=(R²/2)*(π*α/180 -Sinα) - формула.
В нашем случае α=<PKJ =120°.
Skop=(36/2)*(π*120/180 -√3/2)
Skop=(12π-9√3)см².
Искомая площадь равна
S=Sк-Sapk-Skop = 36π-27√3-12π+9√3 = (24π-18√3)см².