Из условия известно, что один угол параллелограмма в 2 раза больше другого. Для того, чтобы найти меньший угол параллелограмма мы должны вспомнить свойства углов параллелограмма и чему равна сумма углов четырехугольника.
Итак, у параллелограмма противоположные углы равны между собой.
Итак, одну пара углов обозначим с переменной x, тогда вторая пара углов равна 2x.
Сумма углов четырехугольника равна 360°.
x + x + 2x + 2x = 360;
6x = 360;
x = 360 : 6;
x = 60° меньший угол параллелограмма,
Тогда больший равен 60 * 2 = 120°.
Дано:
MNP - треугольник
<M = 35
<N = 90
MN = 14 см
Найти:
PN = ?
MP = ?
< P = ?
Так, как в треугольнике сумма всех углов равна 180°, то>
<P = 180 - (<N+<M) = 180 - (35+90) = 180 - 125 = 55°
-------------------------------------------------------------------------------------
ЕСЛИ ВЫ НЕ ПРОХОДИТЕ СИНУСЫ В ДАННЫЙ МОМЕНТ, ТО ДАННОЕ РЕШЕНИЕ НЕ ДЛЯ ВАС!
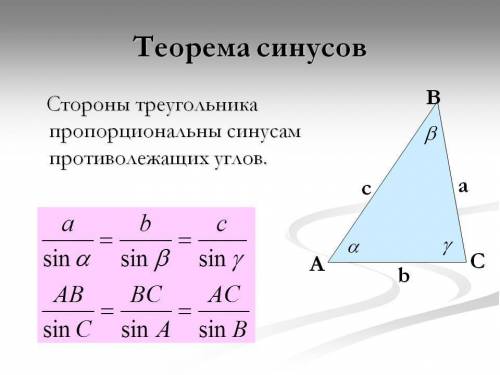
Данную задачу можно решить с теоремы синусов, которая утверждает, что стороны треугольника пропорциональны синусам противолежащих углов.
Значит:
MN/sin(<P) = NP/sin(<M) = MP/sin(<N) =>
14/sin(55) = NP/sin(35) , 14*sin(35)/sin(55) = NP
14/sin(55) = MP/sin(90), 14*sin(90) / sin(55) = MP = 14/sin(55)
PN = 14*sin(35)/sin(55)
MP = 14/sin(55)
<P = 55°
Вроде правильно....
Ребро AD перпендикулярно плоскости грани DD₁C₁C, так как AD⊥DC и AD⊥DD₁.
AD║BC как стороны квадрата,
ВС║В₁С₁ как стороны квадрата, значит
AD║B₁C₁, значит и В₁С₁⊥(DD₁C₁).
Чтобы построить сечение, перпендикулярное грани DD₁C₁C, надо через точку М провести МР║AD и в грани ВВ₁С₁С произвольный отрезок НК║В₁С₁ (параллельные плоскости пересекаются секущей плоскостью по параллельным прямым).
МРНК - сечение, перпендикулярное грани DD₁C₁C.
МР║AD, значит AD║(MPH),
значит и В₁С₁║(МРН).