ответ: 60°
Объяснение:
Угол между плоскостями – двугранный угол. Его величина определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём.
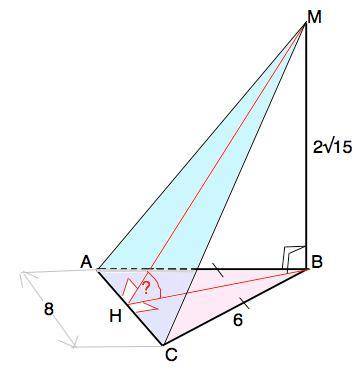
Отрезок МВ по свойству перпендикуляра к плоскости перпендикулярен любой прямой в этой плоскости. ВН - высота ∆ АВС ⇒ ∆ МВН - прямоугольный.
В плоскости АВС отрезок ВН перпендикулярен АС ( ребру двугранного угла), в плоскости АМС - наклонная МН, АС по т. о 3-х перпендикулярах. Угол МНВ - искомый.
ВН - высота и медиана ∆ АВС, поэтому АН=НС=4 (см).
По т.Пифагора ВН=√(ВС²-СН²)=√(36-16)=2√5 (см)
tg MHB=МВ:НВ=(2√15):2√5=√3
√3–тангенс 60°. Угол МНВ=60°
Угол АОС =150°. Смежные с ним углы АОД и СОЕ равны 180° - 150° = 30°.
Медианы треугольника точкой пересечения О делятся в отношении 2:1, начиная от вершины, поэтому АО = 2см, а ОЕ = 1см.
Поэтому же ОД = х , а СО = 2х
Медианы делят треугольник на 6 равновеликих (равных по площади) треугольников, поэтому площадь треугольника АОD
S(AOD) = 1/6 S(ABC) = 12 : 6 = 2(см²)
Площадь треугольника AOD можно вычислить и иначе:
S(AOD) = 0.5 · AO · OD · sin 30° = 0.5 · 2 · x · 0.5 = 0.5x
0.5x = 2 → x = 4(см) - это OD, а ОС = 2х = 8(см)
СD = OD + OC = 4 + 8 = 12(cм)
ответ: 12см
Решение во вложении.