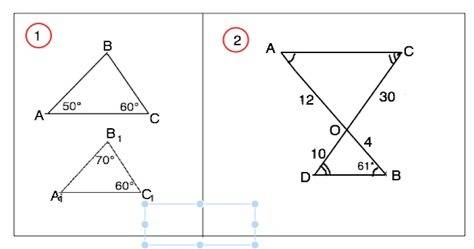
1) Сумма углов треугольника 180°. В ∆ АВС угол В=180°-50°-60°=70°. В ∆ А1В1С1 угол А1=180°-708-608=50°. Треугольники АВС и А1В1С1 подобны по равенству всех углов.
2) По условию АС║BD, АВ и СD - секущие. Образовавшиеся при пересечении секущими параллельных прямых накрестлежащие углы равны. ⇒ ∠СAО=∠DBO=61°. Треугольники АОС и BOD подобны по равенству накрестлежащих углов, а стороны, содержащие вертикальные углы при О - пропорциональны. k=АО:ВО=12:4=3, k=СО:DO=30:10=3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. S(AOC):S(BOD)=k²=3²=9
2.Допустим треугольника АВС. АС- основание. Проведем высоту ВН. Т.к. треугольник равнобедренный, она (высота) будет являться медианой и биссектрисой. Получили два прямоугольных треугольника: АВН и НВС. АН=НС 4дм/2дм=2дм. По теореме Пифагора ищем АН.
√4²-2²=√12=2√3 дм. Это и будет являться радиусом описанной окружности.
3. Номер три на фотке
P.S. за 3 задания маловато, побольше бы :)