8 см
Объяснение:
Пусть дан треугольник АВС. АС=30см. Обозначим точки касания вписанной окружности и сторон треугольника АС, АВ и ВС соответственно К, Т, Р.
Тогда по условию задачи ВТ=12 см и АТ=14 см
Тогда АТ=АК= 14 см
КС= АС-АК=30-14=16 см
КС=РС=16 см
ВР=ВТ=12 см
Тогда АВ=АТ+ВТ=12+14=26 см, ВС =ВР+РС=12+16=28 см
Тогда периметр Р= 26+28+30=84 см
Тогда полупериметр р=Р:2=84:2=42
Тогда площадь треугольника по теореме Герона
S=sqrt(p*(p-a)*(p-b)*(p-c))= sqrt(42*12*14*16)=336
С другой стороны площадь треугольника может быть вычислена по формуле S=p*r=42*r=336
=> r=336/42
r=8
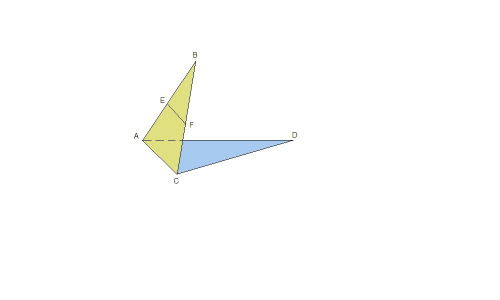
Условие задачи неполное: не сказано, на каких сторонах треугольника АВС лежат точки Е и F.
Вероятно, Е ∈ АВ и F ∈ ВС, так как при любом другом расположении среди предложенных вариантов ответов нет правильного.
а) AC и BF - пересекающиеся;
б) BE и DC - скрещивающиеся, так как
DC ⊂ ADC,
BE ∩ ADC = A,
A ∉ DC, ⇒ по признаку скрещивающихся прямых, прямые ВЕ и DC - скрещивающиеся.
в) AD и FC - скрещивающиеся, так как
AD ⊂ ADC,
FC ∩ ADC = C,
C ∉ AD, ⇒ по признаку скрещивающихся прямых, прямые AD и FC - скрещивающиеся.
г) EF и AC - параллельные (по свойству средней линии)
д) EF и AD - скрещивающиеся, так как
EF ⊂ ABC,
AD ∩ ABC = A,
A ∉ EF, ⇒ по признаку скрещивающихся прямых, прямые EF и AD - скрещивающиеся.
ответ: 4) б, в, д.