ответ: треугольнике АВС угол АСВ опирается на диаметр АВ, следовательно его величина равна 900, а треугольник АВС прямоугольный.
По условию, СМ перпендикулярно АВ, тогда отрезок СН - высота СН треугольника АВС. В прямоугольном треугольнике АСН катет СН лежит против угла 300, а следовательно равен половине длины гипотенузы АС.
СН = АС / 2 = 8 / 2 = 4 см.
Диаметр окружности АВ делит хорду СМ пополам, так как они перпендикулярны, тогда длина хорды СМ = 2 * СН = 2 * 4 = 8 см.
ответ: Длина хорды СМ равна 8 см.
Объяснение:
Для решения нужно найти сторону основания и апофему.
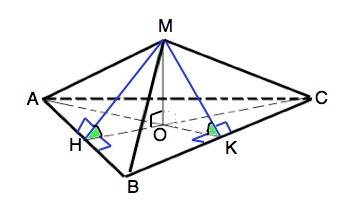
Основание правильной треугольной пирамиды МАВС - равносторонний треугольник АВС.
СН=5 ⇒
СВ=СН:sin60°=5:√3/2=10/√3
Вершина правильной пирамиды проецируется в центр основания,
т.е. в точку пересечения медиан ∆ АВС.
По свойству медиан т.О делит СН в отношении СО:ОН=2:1 =>
ОН=CH:3=5/3
Данный по условию двугранный угол - угол между боковой гранью и основанием, а ребром его является сторона основания.
Градусной мерой двугранного угла является величина линейного угла, стороны которого – лучи с общим началом на ребре двугранного угла, проведенные в его гранях перпендикулярно ребру.
Наклонная МН⊥АВ, её проекция СН⊥АВ, ⇒ угол МНО=45°
∆ МОН- прямоугольный.
cos45°=√2/2
Апофема МН=ОН:cos45°=(5/3):(√2/2)
S(ABC)=CH•AB:2=5•5/√3=25/√3
S(бок)=3•МН•АВ=3•10/(3√2)•0,5•10/√3=25√2/√3
S(полн)=S (осн)+S(бок)
S(полн)=25/√3+25√2/√3 =25•(1+√2):√3= ≈ 34,846 см²