Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
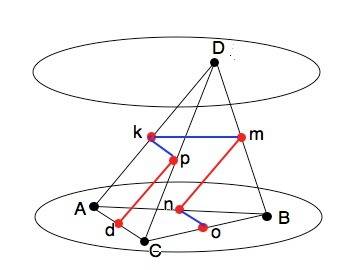
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
Пусть сторона основания - а, высота(боковое ребро) - h.
Тогда из условия: h = a*tg60 = акор3
Площадь одной боковой грани:
12кор3 = a*h = a^2*кор3
Отсюда a^2 = 12, a = 2кор3, h = 2*3 = 6
Площадь основания:
S = (a^2кор3)/4 = 3кор3
Объем:
V = Sосн*h = 3кор3 * 6 = 18кор3.
ответ: 18кор3