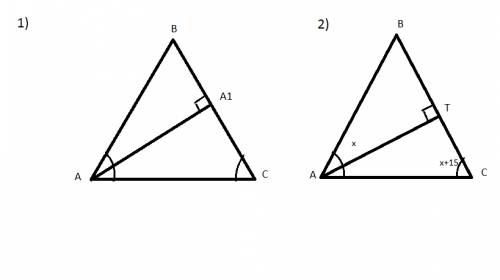
1)Найдем угол В=180-(50+50)=80 градусов. Проведя высоту получим два прямоугольных треугольника. Рассмотрим прямоугольный треугольник АВА1:
Т к угол АА1В=90 градусов, а угол В=80 градусов, то угол ВАА1=180-(90+80)=10градусов.
ОТВЕТ: 10 градусов
2) Пусть угол ВАТ=х, тогда ВСА=ВАС=15+х градусов. Найдем угол ТАС=уголВАС-уголВАТ=15+х-х=15градусов. Т к проведена высота АТ, угол АТС=90 градусов, тогда угол ВСА=180-(90+15)=75градусов. Т к треугольник равнобокий то угол ВСА=ВАС=75 градусов. А угол АВС=180-(75+75)=30 градусов.
1) 256 см²
2) 40 дм²
Объяснение:
1)
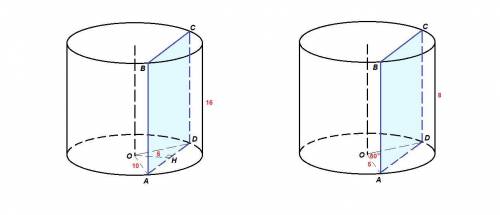
Сечение цилиндра, параллельное его оси, - прямоугольник, одна сторона которого равна высоте цилиндра, а другая - AD - хорда основания.
Проведем ОН ⊥ AD. Сечение параллельно оси, значит отрезок АВ перпендикулярен плоскости основания. Значит АВ⊥ОН. Тогда ОН⊥(АВС), т.е. ОН = 6 см - расстояние от оси до плоскости сечения.
ΔАОН: ∠АНО = 90°, по теореме Пифагора
АН = √(АО² - ОН²) = √(10² - 6²) = √(100 - 36) = √64 = 8 см
ΔAOD равнобедренный (ОА = OD как радиусы), значит ОН - высота и медиана.
AD = 2 · AH = 2 · 8 = 16 см
Sabcd = AD · AB = 16 · 16 = 256 см²
2)
Если сечение перпендикулярно основанию, то оно параллельно оси цилиндра и имеет форму прямоугольника, одна сторона которого равна высоте, а другая - AD - хорда, отсекающая от окружности основания дугу в 60°.
∠AOD = 60°, так как центральный угол равен дуге, на которую опирается.
ΔAOD равнобедренный (AO = OD как радиусы) с углом 60°, значит он равносторонний.
AD = AO = 5 дм
АВ = 8 дм
Sabcd = AB · AD = 5 · 8 = 40 дм²
ВС=3см
АВ=2см
АС=4 см
Решение:
3см+2см=5см
5см>4см
Точки А, В и С не принадлежат одной прямой.