a - сторона квадрата, вписанного в малый сегмент, b - в большой.
(a/2)^2 + (a + h)^2 = R^2; (b/2)^2 + (b - h)^2 = R^2;
5*a^2/4 + 2*a*h + h^2 = R^2; 5*b^2/4 - 2*b*h + h^2 = R^2;
a^2 + (8/5)h*a - (R^2 - h^2) = 0; b^2 - (8/5)h*b - (R^2 - h^2) = 0
a = -(4/5)*h + корень(((4/5)*h)^2 + (R^2 - h^2)); (отрицательный отброшен)
b = (4/5)*h + корень(((4/5)*h)^2 + (R^2 - h^2)); (отрицательный отброшен)
b - a = (8/5)*h;
Возможно, это можно как то увидеть с чисто геометрического построения, но я не нашел ...
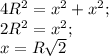
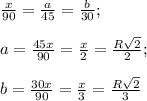
1) если один угол = х°, то другой = 2х (по условию)
х + 2х = 180
3х = 180
х = 60
2х = 120
Противолежащие углы параллелограмма равны,
⇒ углы параллелограмма = 60°; 120°; 60°; 120°
2) Если углы по одной стороне параллелограмма относятся как 4 : 5, значит один угол = 4 частям, то другой угол равен 5 частям.
⇒ 4 + 5 = 9 (частей) составляют 180°
180 : 9 = 20° приходятся на одну часть
20 * 4 = 80° - это один угол
20 * 5 = 100° - это другой угол,
а т.к. противолежащие углы равны, то углы параллелограмма =
80°; 100°; 80°; 100°.