А1. ответ: 4.
А2. ответ: 4.
А3. ответ: 3.
А4. ответ: 1.
В1. Дано: ΔАВС, АВ = ВС = АС + 5 см, Р = 34 см.
Найти: АВ.
Решение: Пусть АС = х см, тогда АВ = ВС = х + 5,
x + (x + 5) + (x + 5) = 34
3x + 10 = 34
3x = 24
x = 8
АС = 8 см
АВ = ВС = 8 + 5 = 13 см
ответ: боковая сторона 13 см.
В2. Дано: ΔАВС, АВ = АС, АМ - медиана, Pabc = 40 см, Pabm = 33 см.
Найти: АМ.
Pabm = 33 см
АВ + ВМ + АМ = 33
2 · (АВ + ВМ + АМ) = 66
Так как АВ = АС, а ВМ = СМ, то
2АВ + 2ВМ + 2АМ = 66
АВ + АС + ВС + 2АМ = 66
2АМ = 66 - (АВ + АС + ВС) = 66 - Pabc = 66 - 40 = 16
AM = 16/2= 8 см
С1. 1) Если сумма равных сторон равна 26 см, то боковые стороны равны по 13 см, а основание - 10 см.
2) Обозначим боковые стороны а и b, основание - с.
а + с = 26 см
Рabc = 2а + с = 36 см
с = 36 - 2а
с = 26 - а
26 - a = 36 - 2a
a = 10 см
c = 16 см
ответ: 13 см, 13 см, 10 см или 10 см, 10 см, 16 см.
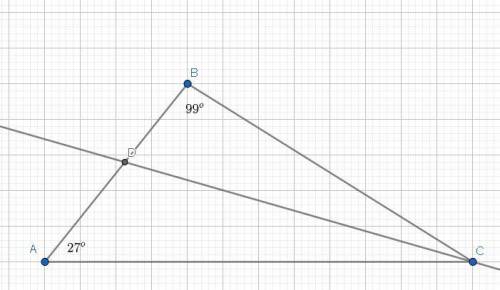
1. Для начала найдём все углы треугольника ΔABC.
<A = 27°; <B = 99° ⇒ <C = 180-(99+27) = 54°.
Так как биссектриса CD — делит угол <C на 2 равные части, то: <DCA = 54/2 = 27°.
Тоесть: <DAC == <DCA ⇒ DA == DC, что и означает, что треугольник ΔADC — равнобёдренный, так как боковые стороны равны.
2.
Угол — противоположный стороне DB — это <BCD, который в треугольнике ΔDBC — считается самым маленьким углом — 27°.
А сторона, противолежащая самому маленькому углу — считается самой маленькой стороной в определённом треугольнике.
В треугольнике ΔADC — опять же, самый маленький угол — <A (27°), а противолежащая ему сторона — DC, которая самая маленькая в треугольнике ΔADC.
И так как углы совпадают, то стороны равны, тоесть BD == CD.
BH = 7см, как перпендикуляр к прямой CD.
ΔBHC - прямоугольный (∠BHC=90°), а ∠HCB=30°, поэтому BC=2·BH=7см·2=14см т.к. BH - катет лежащий напротив угла в 30°.
AD = BC = 14см, как противоположные стороны параллелограмма.
Так же AB = DC = (P-AD-BC):2 = (60-14-14):2 = 30-14 = 16см
∠BAD = ∠BCD = 30°, как противоположный углы параллелограмма.
Так же ∠ABC = ∠ADC = (360°-∠BAD-∠BCD):2 = (360°-30°-30°):2 = 180°-30° = 150°.
AB = 16см; BC = 14см; DC = 16см; AD = 14см;
∠BAD = 30°; ∠ABC = 150°; ∠BCD = 30°; ∠ADC = 150°.