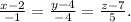Question

Даны четыре точки a1(x1,y1,z1), a2(x2,y2,z2) a3(x3,y3,z3), a4(x4,y4,z4).составить уравнения: а)плоскости а1 а2 а3; б)прямой а1 а2; в)прямой а4м перпендикулярной к плоскости а1 а2 а3; г)прямой а3 n параллельной прямой а1 а2 д)плоскости проходящей через точку а4 перпендикулярно к прямой а1 а2 а1(6,8,2), а2(5,4,7), а3(2,4,7), а4(7,3,7)

Answer 1

Даны координаты пирамиды: A1(6,8,2), A2(5,4,7), A3(2,4,7), A4(7,3,7).
1) Координаты векторов.
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi; Z = zj - zi
здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;
Например, для вектора A1A2
X = x2 - x1; Y = y2 - y1; Z = z2 - z1
X = 5-6; Y = 4-8; Z = 7-2
A1A2(-1;-4;5)
A1A3(-4;-4;5)
A1A4(1;-5;5)
A2A3(-3;0;0)
A2A4(2;-1;0)
A3A4(5;-1;0)

2) Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой:
a = √(X² + Y² + Z²).
Нахождение длин ребер и координат векторов.
Вектор А1A2={xB-xA, yB-yA, zB-zA}      -1 -4  5        L = 6,480740698.
Вектор A2A3={xC-xB, yC-yB, zC-zB}      -3  0  0       L =3.
Вектор А1A3={xC-xA, yC-yA, zC-zA}      -4 -4  5       L = 7,549834435.
Вектор А1A4={xD-xA, yD-yA, zD-zA}       1 -5  5       L =7,141428429.
Вектор A2A4={xD-xB, yD-yB, zD-zB}       2 -1  0       L = 2,236067977.
Вектор A3A4={xD-xC, yD-yC, zD-zC}       5 -1  0       L = 5,099019514.  

3) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:
$\frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} = \frac{z-z_1}{z_2-z_1}$
Параметрическое уравнение прямой:
x=x₀+lt
y=y₀+mt
z=z₀+nt
Уравнение прямой A1A2(-1,-4,5)
$\frac{x-6}{-1}= \frac{y-8}{-4}= \frac{z-2}{5} .$
Параметрическое уравнение прямой:
x=6-t
y=8-4t
z=2+5t.

4) Уравнение плоскости А1А2А3.

x-6    y-8    z-2

-1      -4      5
-4      -4     5   = 0
(x-6)((-4)*5-(-4)*5) - (y-8)((-1)*5-(-4)*5) + (z-2)((-1)*(-4)-(-4)*(-4)) =
= - 15y - 12z + 144 = 0
Упростим выражение: - 5y - 4z + 48 = 0.

5) Уравнение прямой А4М, перпендикулярной к плоскости А1А2А3, - это высота из точки А4 на основание пирамиды.
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C).
 $\frac{x-x_0}{A} = \frac{y-y_0}{B} = \frac{z-z_0}{C} .$
Уравнение плоскости A1A2A3: - 5y - 4z + 48 = 0.
Уравнение А4М: $\frac{x-7}{0}= \frac{y-3}{-5}= \frac{z-7}{-4}.$

6) Уравнение плоскости, проходящей через точку перпендикулярно вектору A1A2.
Уравнение плоскости, проходящей через точку M₀(x₀, y₀, z₀) перпендикулярно вектору N = (l,m,n), имеет вид:
l(x- x₀) + m(y- y₀) + n(z- z₀) = 0
Координаты точки A4(7;3;7)
Координаты вектора A1A2(-1;-4;5)
-1(x - 7) + (-4)(y - 3) + 5(z - 7) = 0
Искомое уравнение плоскости:
-x - 4y + 5z-16 = 0.

7) Уравнение прямой А3N, параллельной прямой А1А2.

Необходимая для решения точка А3(2; 4; 7) задана по условию, а направляющий вектор для искомой прямой возьмём тот же, что для прямой А1А2, так как они параллельны: n=(-1;-4;5). 

ответ: $\frac{x-2}{-1}= \frac{y-4}{-4}= \frac{z-7}{5} .$