ответ: кут VUT = 45°, трикутник TUV = трикутнику TSV
Объяснение:
1) За умовою трикутник SVU - прямокутний.
Якщо VT - бісектриса кута V, тоді
Кут SVT = куту UVT = 45°(бісектриса ділить кут навпіл)
Знаходимо кути S і U:
Кут S = 180° - (90 ° + кут SVT) = 180° - 135° = 45°(сума кутів трикутника 180°)
Кут U = 180° - (90° + кут UVT) = 180° - 135° = 45°(сума кутів трикутника 180°)
(Кут U це і є кут VUT)
2) Розглянемо трикутники TUV і TSV
В них:
1. VT - спільна сторона
2. Кут UVT = куту SVT(однакові)
3. Кут S = куту U (однакові)
Отже, трикутники TUV і TSV однакові(за стороною і двома кутами)
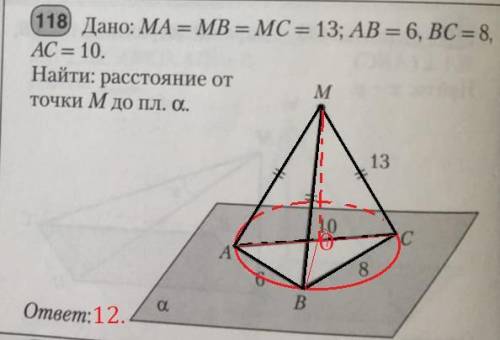
Точка M, равноудалена от вершин треугольника ABC, поэтому она лежит на перпендикуляре к (ABC), который восстановлен из центра (O) описанной около ΔABC окружности. Треугольник со сторонами 6, 8, 10 является египетским (10²=6²+8²), поэтому ∠B=90°, а значит центр описанной лежит на середине AC. И её радиус равен AC:2=10:2=5.
Как было сказано ранее MO⊥(ABC).
Рассмотри прямоугольный ΔAOM (∠O=90°): AO=5; AM=13. Найдём второй катет MO (расстояние от M до α) по теореме Пифагора (хотя тут опять Пифагорова тройка 5, 12, 13).
MO=√(13²-5²) = √((13+5)(13-5)) = √(18·8) = √(3²·4²) = 12
ответ: 12.
Найти:
А) длину отрезка AB:
|АВ| = √((-5-3)²+(6+4)²+(0-2)²) = √(64+100+4) = √168 = 2√42 ≈ 12,96148.
Б) координаты средины отрезка АВ (пусть это точка С):
С = ((3-5)/2=-1; (-4+6)/2=1; (2+0)/2=1) = (-1; 1; 1).
В) точку оси Оx (пусть это точка М), равноудаленную от точек А и В.
Обозначим координаты точки М(x, y, z).
По заданию Мy = 0, Мz = 0, АМ² = ВМ².
АМ² = (х-3)²+(0-(-4))²+(0-2)² = х²-6х+9+16+4 = х²-6х+29.
ВМ² = (х+5)²+(0-6)²+(0-0)² = х²+10х+25+36+0 = х²+10х+61.
Приравняем: х²-6х+29 = х²+10х+61.
16х = -32.
х = -32/16 = -2.
ответ: точка М(-2; 0; 0).