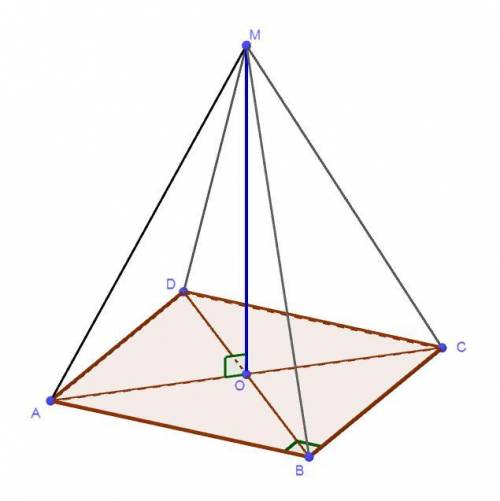
Точка пересечения диагоналей квадрата является центром квадрата. Т.к. из него проведена перпендикулярная прямая, значит расстояние от т. О до вершин квадрата будет одинаковое. Следовательно, нам нужно найти одно такое расстояние, чтобы знать все.
Стороны квадрата (а) равны. Диагонали у квадрата равные (d), и точк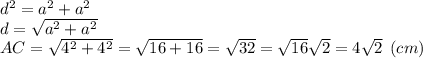
а пересечения делит их пополам.
Р-м ΔAOM:
∠O = 90°, AO — половина диагонали, OM — перпендикуляр к плоскости квадрата. АМ — наклонная.
AO = d/2
Ищем, чему равна диагональ квадрата:
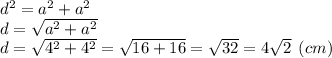
AO = (4√2)/2 = 2√2 см
Теперь можем найти длину отрезка AM
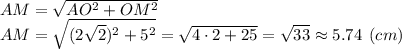
ответ: Расстояние равно √33 см, или приблизительно 5,74 см.
АВ - первая сосна,
CD - вторая сосна,
AD - расстояние между ними.
Если считать, что сосны растут перпендикулярно земле, получаем прямоугольную трапецию с основаниями АВ и CD, в которой большая боковая сторона ВС - искомая величина.
Проведем СН - высоту трапеции.
СН = АD = 20 м, как расстояния между параллельными прямыми,
СН║AD как перпендикуляры к одной прямой, значит AHCD - прямоугольник, ⇒
АН = CD = 12 м
ВН = АВ - АН = 27 - 12 = 15 м
Из прямоугольного треугольника ВСН по теореме Пифагора:
ВС² = ВН² + НС² = 15² + 20² = 225 + 400 = 625
ВС = 25 м