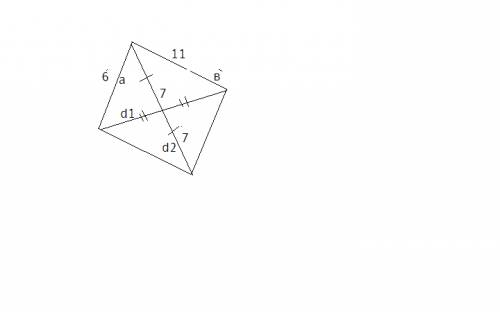
Достроим треугольник до параллелограмма, тогда медиана будет половина диагонали данного параллелограмма.
По формуле a^2+b^2=(d1+d2)/2. , где а и в стороны, можно найти неизвестную диагональ d2. а известная диагональ d1=2*7=14(т . е две медианы)
36+121=(196+d2^2); d2^2=314-196=118; d2=√118
Зная стороны треугольника можно найти угол между сторонами по теореме косинусов.
cosβ=(36+121-((√118)^2)/2*6*11≈0.33
По таблице Брадиса найдем угол
β=71 градус
ответ 71 градус ( Для понятности вложу рисунок , см. вложенный файл)
Выясним соотношения между катетами и гипотенузой треугольника. Пусть гипотенуза равна 2х, тогда один катет равен х(тот, что лежит против угла в 30гр.), а другой 2х · cos 30 = 2x·0.5√3 = x√3/
Радиус вписанной в прямоугольник окружности равен
r = ( a + b - c):2, где а и b -катеты, а с - гипотенуза.
r = ( х + х√3 - 2х):2 = 0,5х(√3 - 1)
0,5х(√3 - 1) = 4
Отсюда х = 8/(√3 - 1)
Периметр треугольника: Р = 2х + х + х√3 = х(3 + √3). Полупериметр р = 0,5х(3 + √3)
Площадь треугольника S = r·p = 4·0,5х(3 + √3) = 2х(3 + √3)
Подставим х = 8/(√3 - 1) и получим
S = 2·(3 + √3)·8/(√3 - 1)
S = 16√3·(√3 + 1)/(√3 - 1)