1) луч
2) лучи обозначаются через две латинские буквы или одной маленькой латинской буквой.
3) дополнительные лучи – это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой
4) угол
5) одной заглавной латинской буквой ( вершина угла ), двумя малыми латинскими буквами ( стороны угла )
6) если его обе плоскости лежат на одной прямой
7) две полуплоскости
8) два угла называются равными - если их можно совместить наложением
9) биссектриса угла — луч с началом в вершине угла, делящий угол на две равные части
10) в градусах
11) 180 градусов
12) острый
13) у которого градус меньше 90
14) у которого градус больше 120
15) 1) равные углы имеют равные величины равные величины 2) если он состоит из двух углов
16) равные углы имеют равные величины
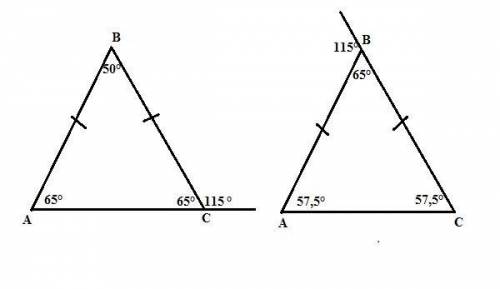
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
90 и 90 и 118 и 60
Так как Трапеция прямоугольная а в трапеции основания равны то тогда в каждой прямоугольной трапеции в угла равны по 90.
Тогда 360-2*90-118=62.