ответ: arctg(√2tgα).
Объяснение:"Углом между указанными плоскостями MDC и АВС является угол, стороны которого – лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру".
1) ΔДОС: ОД=ОС по свойству диагоналей квадрата,
ОЕ- медиана по условию ⇒ОЕ- высота и ∠ОЕС=90°.
2) ΔОЕС: ∠ОЕС=90°, пусть ДС=а, тогда ОЕ=ЕС=а/2,
ОС²=(а/2)²+(а/2)²=а²/4 + а²/4= 2а²/4= а²/2;
ОC=а:√2= (а√2) :2.
ОМ:ОС=tgα ⇒ ОМ=ОС*tgα= (а√2) :2 * tgα= (а√2*tgα) :2.
3) ΔОМЕ: ОМ⊥ пл.АВС, ОЕ⊂пл.АВС ⇒ ОМ⊥ОЕ.
tg∠ОЕМ = ОМ:ОЕ = (а√2*tgα):2 :а/2= (а√2*tgα):а= √2tgα;
4) ОЕ⊂пл.АВС, ОЕ⊥ДС, МЕ- наклонная к пл.АВС,
ОЕ- проекция МЕ на пл.АВС ⇒
⇒ по теореме о трёх перпендикулярах МЕ ⊥ ДС.
пл.АВС ∩ пл.ДМС= ДС, МЕ ⊂ пл.ДМС и МЕ⊥ДС,
ОЕ ⊂ пл.АВС и ОЕ⊥пл. АВС ,
значит ∠(МДС;АВС)=∠ОЕМ= arctg(√2tgα).
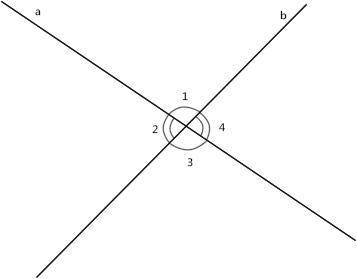
a ∩ b.
Один из углов в 4 раза > другого.
Найти :Больший угол = ?
Решение :При пересечении двух прямых образуются четыре угла.
∠1 = ∠3, ∠2 = ∠4 (это пары вертикальных углов. Они равны между собой по свойству вертикальных углов).
Пусть ∠2 = х.
Тогда, по условию задачи, один из углов должен быть равен 4х.
Естественно, что ∠4 ≠ 4х, так как уже ∠4 = х по выше сказанному.
Тогда пусть ∠1 = 4х.
∠1 и ∠2 - смежные (по определению).
Сумма смежных углов равна 180°.Отсюда :
∠1 + ∠2 = 180°
4х + х = 180°
5х = 180° ⇒ х = 180° : 5 = 36°
4х = 4*36° = 144°.
(Естественно, что за 4х мы брали самый больший угол, поэтому в ответ пойдёт значение 4х).
ответ :144°.