Биссектриса угла a параллелограмма abcd пересекает сторону bc в точке k. найдите периметр параллелограмма, сли bk=5, ck=14. биссектриса угла a параллелограмма abcd пересекает сторону bc в точке k. найдите периметр параллелограмма, сли bk=8, ck=13. биссектриса угла aa параллелограмма abcd пересекает сторону bc в точке k. найдите периметр параллелограмма, сли bk=3, ck=19. биссектриса угла aa параллелограмма abcd пересекает сторону bc в точке k. найдите периметр параллелограмма, если bk=6 , ck=10.

👇

Ответ:

vitalikobukhov

10.03.2023

Решение во всех задачах одинаково, но только нужно поменять цифры
Биссектриса угла a параллелограмма abcd пересекает сторону bc в точке k. найдите периметр параллелог

Биссектриса угла a параллелограмма abcd пересекает сторону bc в точке k. найдите периметр параллелог

4,5(50 оценок)

Открыть все ответы

Ответ:

Аянезнаю11

10.03.2023

Задача 6

В ΔАВС , АВ=ВС, АЕ -биссектриса, Е∈ВС. Найти Р( АВС), если ВС-АС=8 и ВЕ:ЕС=3:2.

Решение.

Пусть одна часть х. Тогда ВЕ=3х, ЕС=2х ⇒ ВС=5х ⇒ АВ=5х , т.к треугольник равнобедренный.

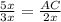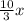По т. о биссектрисе треугольника $\frac{AB}{BE} =\frac{AC}{CE}$ , тогда $\frac{5x}{3x} =\frac{AC}{2x}$ ⇒ AC= $\frac{10}{3}x$ .

По условию ВС-АС=8 , поэтому 5х-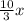 $\frac{10}{3}x$ = 8 или $\frac{5}{3}x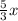$ =8 или х=4,8.

ВС=5*4,8=24 , АВ=24 , АС=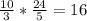 $\frac{10}{3}*\frac{24}{5} =16$ .

Р=24+24+16=64.

Задача 8

Стороны треугольника относятся как 2:3:3 . Найти периметр треугольника , если основание на 5 единиц меньше боковой стороны.

Решение .

Дан ΔАВС. АВ=ВС . Пусть одна часть х. Тогда АВ=ВС=3х, АС=2х .

По условию АС меньше АВ на 5, т.е АВ-АС=5.

Получим 3х-2х=5 или х=5 . Тогда АВ=ВС=3*5=15, АС=2*5=10 .

Р=15+15+10=40.

Задача 9

Угол при вершине равнобедренного треугольника равен 120°. , высота , опущенная на основание, равна 6 .Найти периметр треугольника .

Решение .

Дан ΔАВС , АВ=ВС ,ВН⊥АС , ∠АВС=120°.

1) Высота равнобедренного треугольника является биссектрисой ⇒∠АВН=60° .

2) ΔАВН -прямоугольный , по свойству углов ∠А=90°-60°=30°.

Против угла в 30° , лежит катет равный половине гипотенузы , т.е ВН=1/2*АВ ⇒ АВ=12 ⇒ВС=12, т.к треугольник равнобедренный.

По т. Пифагора АН²=АВ²-ВН² или АН²=12²-6² или АН=√18*6=6√3.

3) Высота равнобедренного ΔАВС является медианой, значит АН=НС=6√3 ⇒АС =12√3.

4)Р=12√3+12+12=24+12√3.

4,4(20 оценок)

Ответ:

Pavro1

10.03.2023

ответ: S=20см²

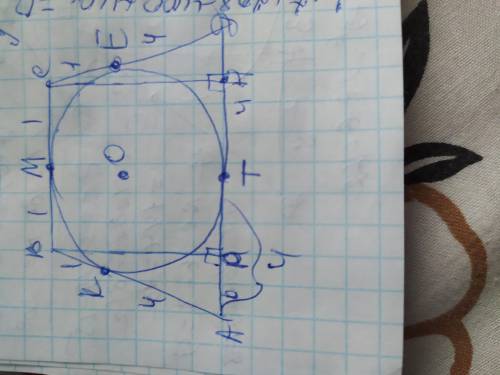
Объяснение: Обозначим вершины трапеции А В С Д а точки касания К М Е Т, центр окружности О. стороны трапеции являются касательными к вписанной окружности и отрезки касательных соединяясь в одной вершине, равны от вершины до точки касания, поэтому ВК=ВМ=МС=СЕ=1см;

АК=АТ=ЕД=ТД=4см. Сложим эти цифры и получим стороны трапеции:

АВ=СД=4+1=4см; ВС=1+1=2см;

АД=4+4=8см.

Проведём из вершин верхнего основания к АД две высоты ВР и СН. Они делят АД так что РН=ВС=2см. Так как трапеция равнобедренная то:

АР=ДН=(АД-ВС)/2=(8- 2)÷2=6÷2=3см

АР=ДН=3см. Рассмотрим полученный ∆СДН. В нём СД -гипотенуза, а СН и ДН- катеты. Найдём высоту СН по теореме Пифагора: СН²=СД²-ДН²=

=5²-3²=25-9=16; СН=√16=4см

СН=4см. Теперь найдём площадь трапеции зная высоту и оба основания по формуле:

S=(BC+AД)/2×СН=

=(2+8)/2×4=10÷2×4=5×4=20см²

S=20см²