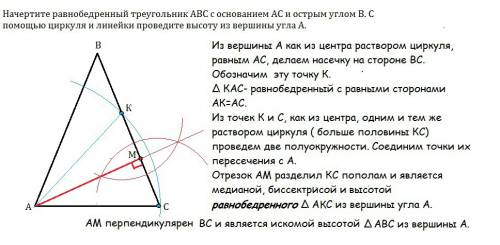
Построение сводится к проведению перпендикуляра из точки к прямой.
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
Пусть из точки O проведены наклонные OA=2 и OB=4. Проведем перпендикуляр OH к плоскости, длину которого и нужно найти. Проекция OA на плоскость равна HA, а проекция OB на плоскость равна HB. Пусть HA=x, HB=7x. Прямоугольные треугольники OHB и OHA имеют общий катет OH. По теореме Пифагора OH=OB^2-BH^2=OA^2-AH^2. Тогда OB^2-BH^2=OA^2-AH^2. 16-49x^2=4-x^2. 12=48x^2, x^2=1/4, x=1/2. Тогда по теореме Пифагора можно найти OH из треугольника OAH, в котором OA=2, AH=1/2. OH=sqrt(4-1/4)=sqrt(15)/4