60√3 см^2
Объяснение:
назвемо трапецію ABCD
S =
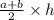
, де S - площа трапеції, a,b - основи, h - висота проведена до основи.
проведемо висоту. назвемо її ВК.
Розглянемо трикутник АВК.
кут К = 90°, отже трикутник прямокутний.
кут А = 60°, за умовою.
за формулою суми кутів трикутника, маємо:
кут В = 180° - 90° - 60° = 30°
за теоремою катета проти кута 30°, маємо:
АК = 12/2 = 6 (см)
знайдемо ВК. за теоремою Піфагора, маємо:
ВК^2 = АВ^2 - АК^2.
ВК^2 = 144 - 36 = 108
ВК = √108 = 6√3
тепер, знайдемо більшу основу.
4+6+6= 16 (см)
підставляємо у формулу:
(4 + 16)/2 × 6√3 = 60√3 (см^2).
1. Так как АВ=ВС, то треугольник равнобедренный
Сумма углов треугольника равна 180°, тогда <В= 180-<А+<С= 180-(50+50) = 80°
У равнобедренного треугольника высота выступает медианой и биссектрисой (в данном случае биссектрисой) тогда <АВМ=<СВМ=80:2=40°
2. Так как АВ=ВС то треугольник равнобедренный.
Так как третья сторона равна сумме двух остальных, то АС=АВ+ВС= 10 см
3. <С=180-125=55°, как смежные
Так как АВ=ВС, тогда треугольник равнобедренный
<А=<С=55°
Сумма углов треугольника равна 180°, <В=180-(55+55)=70°
4. <В= 180-120=60°, как смежные
<С=180-110=70°,как смежные
Сумма углов треугольника равна 180°, тогда <В=180-(70+60)= 50°
5. <С=180-85=95°, Как смежные
<А=<1=40°, как смежные
Сумма углов треугольника равна 180°, тогда <В=180-(95+40)=45°
Диагонали ромба являются биссектрисами. =>
=> 40+40= 80°
180-80=100 ° тупой угол
Отв: 100°, 80°, 100°, 80°
Задача 2:
верны: а, б
Задача 3:
Дано: треугольник ABC
угол С=90°
АС=СВ=16 см
K пренадлежит AC,N пренадлежит CB, M пренадлежит АВ
Решение:
Точки К и N одинаковой делят АС и СВ
поэтому делим 16 на 2
и из за того что это квадрат, все стороны равны