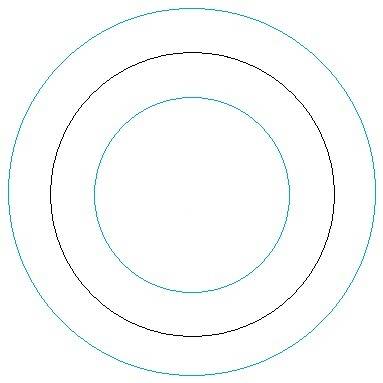
1) Пусть точка M лежит вне окружности. O - центр окружности, точка T - пересечение отрезка OM и окружности. Возьмем на окружности точку T1, не лежащую на OM. В треугольнике MT1O сторона OM меньше суммы двух других сторон (неравенство треугольника),
MT+OT<MT1+OT1 <=> MT<MT1 (OT=OT1, радиусы)
Таким образом, чтобы длина MT была минимальной, T должна лежать на OM. Если M вне окружности, MT=1, OT=2000, то OM=MT+OT=2001. Искомое ГМТ - окружность радиусом 2001 с центром данной окружности.
2) Аналогично доказывается, что если точка M лежит внутри окружности, то искомое ГМТ - окружность радиусом 1999 (OM=OT-MT) с центром данной окружности.

(х-х1) / (х2-х1)= (у-у1)/(у2-у1)
где (х1, у1)-координаты первой точки, (х2, у2)-второй
1) (х-(-1))/(-2-(-1))=(у-(-1))/(-2-(-1)
(х+1)/(-1)=(у+1)/(-1)
х+1=у+1
у=х
2) (х-3)/(0-3)=(у-0)/(4-0)
(х-3)/(-3)=у/4
4х-12=-3у
у=-4/3 х+4
у=-1⅓х + 4