угол MBC = 30°
угол ВCA = 60
Объяснение:
Дано:
АВС - треугольник
АМ = СМ
уг. АВС = 60°
уг. ВМА = 90°
-------------
Найти
уг. МВС - ?
уг. ВСА - ?
Решение
угол ВМА = 90° => уг. ВМС = 90°
т.е. ВМ | АС, а значит,
ВМ - высота, проведенная из вершины В на АС.
Также АМ = МС, а значит
ВМ - медиана, проведенная из вершины В на АС.
Если медиана треугольника является его высотой, то этот треугольник - равнобедренный.
ВМ - высота и медиана ∆АВС, =>
=> ∆АВС - равнобедренный, основание АС =>
=> ВМ - также является биссектрисой ∆АВС, т.е.
уг. АВМ = уг. СВМ
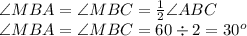
Так, как ∆АВС - равнобедренный, с основанием АС, то углы при основании - равны друг другу
уг. ВАС = уг. АСВ
и равны
угол ВАС = угол ВСА = 1/2 • (180 - угол АВС)
угол ВАС = угол ВСА = 1/2 • (180 - 60) = 60°
а значит ∆АВС - равносторонний.
угол MBC = 30°
угол ВCA = 60°
Стороны равностороннего треугольника обозначим обозначим за Х
Теперь рассмотрим один из прямоугольных треугольников:
гипотенуза равна Х
катет1 равен х/2(это половина стороны,к которой проведена высота)
катет2 равен медиане
по т пифагора найдем гипотенузу(х)
х^2=(x/2)^2+(12 корней из 3)^2
x^2=432+x^2/4 (умножаем все на 4)
4x^2=1728+x^2
4x^2-x^2=1728
3x^2=1728
x^2=1728/3
x^2=576
х=корень из 576
х=24