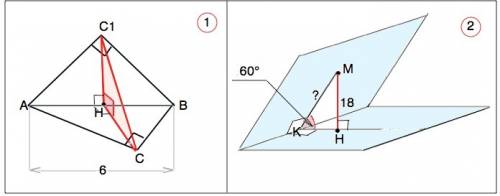
1).
Перпендикулярные плоскости образуют двугранный угол, линейный угол которого образован лучами с общим началом на ребре двугранного угла, проведенными в его гранях перпендикулярно ребру.
Здесь грани - плоскости треугольников АВС и АВС1, ребро двугранного угла – АВ.
НС⊥АВ; НС1⊥АВ, угол СНС1=90° по условию.
∆ АВС и ∆ АВС1 равнобедренные прямоугольные, углы при их общем основании АВ равны 45°, ⇒ они равны по 2-признаку равенства треугольников.
∆ СНС1- прямоугольный. Его катеты равны высотам=медианам равных треугольников. Следовательно, он равнобедренный.
Медиана прямоугольного треугольника равна половине гипотенузы. ⇒
НС=НС1=3
СС1=3•sin45°=3√2 см
2)
Расстояние от точки М до плоскости - длина отрезка МН, проведенного между ними перпендикулярно. МН=18
Расстояние от точки М до ребра двугранного угла - длина отрезка МК, проведенного между ними перпендикулярно.
∆ МКН - прямоугольный. Его гипотенуза МК=МН:sin60°
MK=18:(√3/2)=12√3
Части, на которые биссектриса делит противоположный катет, даны по условию, это 2 и 1
нижний катет примем на 1х
гипотенуза будет в силу пропорциональности будет равна 2х
по теореме Пифагора
(1х)^2 + 3^2 = (2x)^2
9=3x^2
x^2 = 3
x = √3 см
А длину биссектрисы найдём опять же по теореме Пифагора
l^2 = 1^2 + (√3)^2
l^2 = 1+3
l^2 = 4
l = 2 см