Объяснение:
1)У паралелограма 2 однакових гострих і 2 однакових тупих кути, сума 360°, тоді, якщо 2 кути по 52°, то інші два (360°-2*52°)/2=123°
Кути: 52°,52°,123°, 123°
2)протилежні кути паралелограма рівні, отже кожний з цих кутів дорівнює 174°/2=87°, два інші кута дорівнюють по (360°- 174°)/2=93°
Кути : 87°, 87°, 93°,93°
3)Нехай перший кут дорівює х, тоді другий кут дорівнює (х + 28°).
так як сума кутів паралелограма дорівнює 360° , то
(x + x + 28) = 360/2
2x + 28 = 360/2
2x = 180-28
2x = 152
x = 152 : 2
x = 76
х+28=76+28=104
Кути: 76°, 76°, 104°, 104°
4) Так як кути паралелограма попарно рівні, то:
4х+4х+х+х=360°
10х=360°
х=36°
4х= 4*36=144°
Кути: 36°, 36° , 144°, 144°
5) нехай х- одна частина, тоді 4:5 складають
4Х+5Х=360°
9Х= 360°
х=40 ( це одна частина )
4. 4Х=160°/2 =80° ( один кут)
5. 5Х = 200°/2= 100° (другий кут)
Кути: 80°, 80°, 100°, 100°
ответ: ч.т.д.
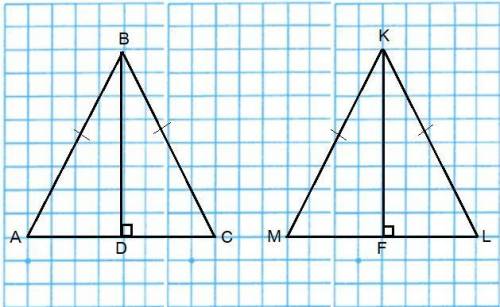
Объяснение: 1) обозначим первый равнобедренный треугольник буквами АВС.
Второй равнобедренный треугольник обозначим буквами MKL.
AC и ML - основания △АВС и △MKL соответственно.
MK = KL = AB = BC, по условию.
Проведём высоту ВD в △АВС к основанию АС и высоту KF в △МКL к основанию ML.
BD = ML, по условию.
Так как BD и KF - высоты △АВС и △MKL соответственно ⇒ △BDA, △BDC, △KFM, △KFL - прямоугольные.
Рассмотрим △BDA, △BDC, △KFM, △KFL:
1) Рассмотрим △BDA и △BDC:
AB = BC, по условию.
BD - общая.
⇒ △BDA = △BDC, по гипотенузе и катету.
2) Рассмотрим △KFM и △KFL:
MK = KL, по условию.
KF - общая.
⇒ △KFM = △KFL, по гипотенузе и катету.
Но так как АВ = ВС = MK = KL и BD = KF, по условию ⇒ △BDA = △BDC = △KFM = △KFL, по катету и гипотенузе.(AB = BC = MK = KL, по условию; BD = KF, по условию)
А так как △BDA = △BDC = △KFM = △KFL ⇒ △ABC = △MKL (MK = AB, по условию; KL = BC, по условию; AC = МL, так как △BDA = △BDC = △KFM = △KFL).
(Также равенство треугольников АВС и KML можно доказать по всем признакам равенства треугольников, исходя из того, что △BDA = △BDC = △KFM = △KFL)
ч.т.д.