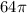Решите 30 1: дан угол aod и две параллельные плоскости альфа и бетта . плоскость a(альфа) пересекает стороны угла oa и od соответственно в точках a1 и d1 плоскость b(бетта) эти стороны пересекает соответственно в точках a2 и d2. oa=9 a1a2=4 ; a2d2=5; d1d2=3 найти: a1d1 и od1 : постройте сечение куба abcda1b1c1d1 плоскостью проходящей через точки a, b, c1 . найдите периметр сечения если ребро куба равно 2 см с рисунком желательно

👇

Увидеть ответ

Ответ:

Maryna03

10.03.2022

А1D1=6 OD1=7

4,7(31 оценок)

Открыть все ответы

Ответ:

aydansuper12

10.03.2022

ответ:

$64\pi$ см³.

Объяснение:

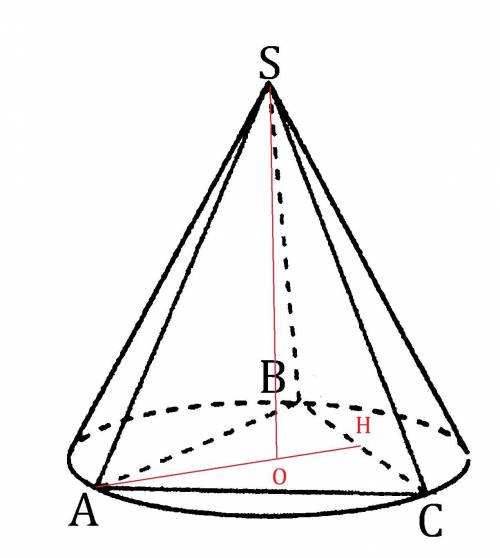
Обозначим данную пирамиду буквами 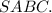SABC.

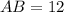AB = 12 см.

Проведём высоту пирамиды SO.

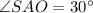
$\angle SAO = 30^{\circ}$

Начертим около этой пирамиды конус.

Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.

=======================================================

Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.

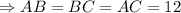$\Rightarrow AB = BC = AC = 12$ см.

Проведём высоту в $\triangle ABC$

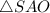$\triangle SAO$ - прямоугольный, так как 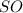- высота пирамиды.

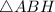$\triangle ABH$ - прямоугольный, так как - высота $\triangle ABC$ .

Так как $\triangle ABC$ - равносторонний ⇒ - высота, медиана и биссектриса

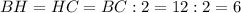BH = HC = BC:2 = 12:2 = 6 см, так как - медиана.

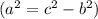Найдём по теореме Пифагора (a^2 = c^2 - b^2) .

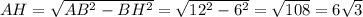$AH = \sqrt{AB^2 - BH^2} = \sqrt{12^2 - 6^2} = \sqrt{108} = 6\sqrt{3}$ см.

Точка 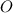- пересечение медиан и делит их в отношении 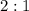2:1 , считая от вершины.

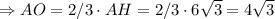$\Rightarrow AO = 2/3\cdot AH = 2/3 \cdot 6\sqrt{3} = 4\sqrt{3}$ см

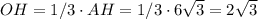$OH = 1/3\cdot AH = 1/3 \cdot 6\sqrt{3} = 2\sqrt{3}$ см.

Также 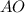- радиус описанной около $\triangle ABC$ окружности.

Рассмотрим 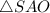$\triangle SAO$

Если угол в прямоугольном треугольнике равен 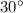$30^{\circ}$ , то напротив лежащий катет равен половине гипотенузы.

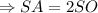
$\Rightarrow SA = 2SO$

Составим уравнение:

Пусть 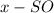x - SO , тогда 2x - SA .

И по теореме Пифагора 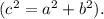(c^2 = a^2 + b^2).

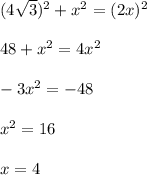
$(4\sqrt{3})^2 + x^2 = (2x)^2\\\\48 + x^2 = 4x^2\\\\-3x^2 =-48\\\\x^2 =16 \\\\x= 4$

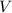конуса = 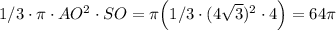$1/3 \cdot \pi \cdot AO^2 \cdot SO = \pi \Big(1/3 \cdot (4\sqrt{3})^2 \cdot 4\Big) = 64\pi$ см³.

Дана правильная треугольная пирамида со стороной основания 12. Боковое ребро пирамиды наклонено к пл

4,4(89 оценок)

Ответ:

mangle56

10.03.2022

дана трапеция ABCD

EM - средняя линия

пересекает диагонали в точках К и N

AC и BD - диагонали

из свойств средней линии трапеции: EM||BC||AD

CM=MD и EM||BC, тогда по теореме Фалеса ( если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне) EM проходит через точку N.

AE=EM и EM||BC, тогда по теореме Фалеса ( если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне) EM проходит через точку K.

Следовательно: AK=CK и DN=BN

можно также доказать через треугольники ABC и DCB - средняя линия трапеции будет средней линией этих треугольников. Средняя линия треугольника делит стороны пополам, значит диагонали пересекаются пополам.

4,7(81 оценок)

Это интересно:

29.07.2022

Как легко и просто найти общий язык с застенчивым парнем, которого вы почти не знаете...

Компьютеры-и-электроника

19.03.2023

Как бесплатно создать сайт: подробный обзор лучших сервисов для начинающих...

Финансы-и-бизнес

23.11.2020

Как купить себе частный остров: преимущества и нюансы покупки...

Дом-и-сад

20.12.2022