Даны точки: A(7; 4; 2), B(-5; 3; -9), C(1; -5; 3), D(7; -9; 1).
Находим векторы AB и AD .
AB = (-12; -1; -11).
AD = (0; -13; -1).
Определяем их векторное произведение.
ABxAD = {aybz - azby; azbx - axbz; axby - aybx} =
= (-1*-1 - -11*-13), (-11-*0 - -12*-1), (-12*-12 - -1*0) = (-142; -12; 156).
Площадь грани ABD равна (1/2)*√((-142)² + (-12)² + 156²) = (1/2)√44644 =
= √11161 ≈ 105,6456 кв.ед.
Находим вектор АС = (-6; -9; 1).
Объём пирамиды ABCD равен (1/6)*(ABxAD)*АС) = (1/6)*(852 + 108 + 156) =
= (1/6)*1116 = 186 куб.ед.
Находим координаты точки Е как середину ребра BD.
Е = (1; -3; -4).
Находим длины отрезков АЕ и СЕ.
AE = 36 49 36 = √121 =11
CE = 0 4 49 =√53 ≈ 7,28011.
Сторона основания АС = √(6² + (-8)² + 12²) =√244 ≈ 15,6205.
Площадь сечения (это треугольник АСЕ) определяем по формуле Герона, так как имеем длины трёх сторон.
Треугольник АEС
a(CE) e(АС) c(АE) p 2p S
7,2801 10,8628 11,0 14,5714 29,14289 37,5133
cos A = 0,7783 cos Е = 0,3496 cos С = 0,31613
Аrad = 0,6788 Еrad = 1,2136 Сrad = 1,24915
Аgr = 38,894 Еgr = 69,5344 Сgr = 71,571
Число 37,5133 примерно равно √5629/2.
Чертёж смотрите во вложении.
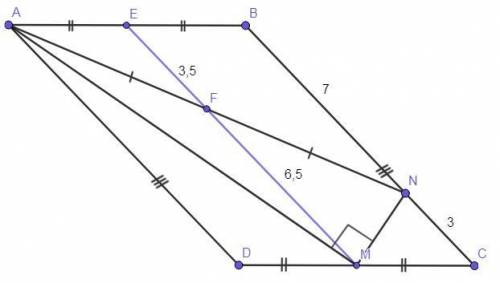
Дано:
ABCD - четырёхугольник.
AD = BC.
AD║BC.
Точка М - середина CD.
Точка N ∈ ВС.
BN = 7.
CN = 3.
∠AMN = 90°.
Найти:
AN = ?
Так как AD = BC и AD║BC, то четырёхугольник ABCD - параллелограмм (по признаку параллелограмма).
Если на одной из двух прямых последовательно отметь несколько равных отрезков и через их концы провести параллельные прямые, то они отсекут на второй прямой равные между собой отрезки (теорема Фалеса). Проведём через точку М прямую МЕ, которая параллельна AD и пересекает сторону AN в точке F. Так как МЕ║AD и AD║ВС, то также МЕ║AD║ВС. Следовательно, по теореме Фалеса, AF = NF, AE = ЕВ.
Рассмотрим четырёхугольник ЕВСМ. Так как ЕМ║ВС (по выше доказанному) и отрезки ЕВ║МС (так как лежат на параллельных прямых), то четырёхугольник ЕВСМ - параллелограмм по определению. Тогда, по свойству параллелограмма, ВС = ЕМ = BN+NC = 7+3 = 10.
Рассмотрим ΔABN. Так как отрезок EF соединяет середины сторон АВ и AN, то EF - средняя линия, причём параллельна стороне BN, а значит, равна её половине (по свойству средней линии треугольника). EF = BN/2 = 7/2 = 3,5.
ЕМ = EF+FM ⇒ FM = ЕМ-EF ⇒ FM = 10-3,5 = 6,5.
Рассмотрим ΔANM - прямоугольный (по условию). FM - медиана, проведённая к гипотенузе, а значит, равна её половине (по свойству прямоугольного треугольника). AN = 2*FM ⇒ AN = 2*6,5 ⇒ AN = 13.
ответ: 13.
х + 3х = 120
4х = 120
х = 120:4
х = 30
3х = 3×30= 90
FEM = 30
MEN = 90