Тетраэдр это многоугольник состоящий из 4 граней, для решения задачи необходимо, чтобы все его рёбра были равны или какое-то ещё дополнительное условие, иначе для решения задачи не хватает данных.
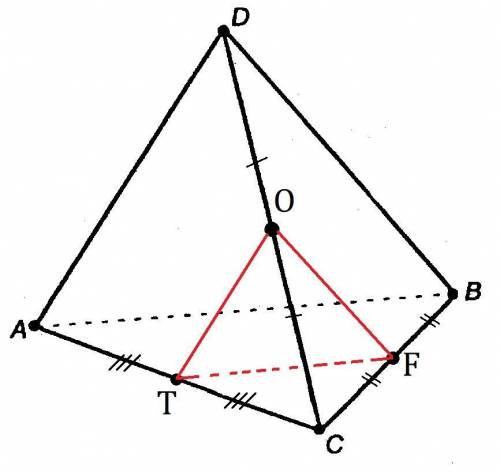
F, O, T - середины ребер BC, DC, AC соответственно. Поэтому FO, OT, TF - средние линии треугольников CBD, CDA, CAB соответственно. А значит, BD=2FO, DA=2OT, AB=2TF.
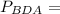 BD+DA+AB = 2FO+2OT+2TF = 2(FO+OT+TF) =
BD+DA+AB = 2FO+2OT+2TF = 2(FO+OT+TF) = 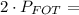 2·12см = 24см.
2·12см = 24см.
ΔBDA - равносторонний (все рёбра тетраэдра равны), поэтому BD=DA=AB=24см:3=8см. Найдём площадь равностороннего треугольника по формуле 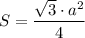 , где a - сторона треугольника.
, где a - сторона треугольника.
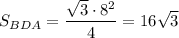 см².
см².
Площадью боковой поверхности, будет площадь любых 3 граней (все грани это равные, равносторонние треугольники).
S(бок.) = 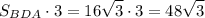 см².
см².
ответ: 48√3 см².
AK = AB sin ß = b sin β
BK = AB cos β = b cos β
SABK = AK * BK / 2 = b2sin β cos β / 2
откуда
SABС = 2SABK = b2sin β cos β
(примем за искомую площадь основания, далее справочно приведем к той же формуле, которая указана по ссылке выше)
Если воспользоваться основными тригонометрическими тождествами, то
b2sin β cos β = 1/2 b2sin 2β = 1/2 b2sin 2β
или как по основной формуле (площади равнобедренного треугольника)
1/2 b2sin 2β = 1/2 b2sin (180 - α) = 1/2 b2sin α
Теперь найдем площадь боковой поверхности пирамиды.
Сначала найдем высоту боковых граней, прилежащих к равным сторонам равнобедренного треугольника, лежащего в основании пирамиды. При этом учтем, что высота пирамиды проецируется в точку О основания, которая одновременно является центром вписанной окружности. Вместе с радиусом вписанной окружности, высота боковой грани образует прямоугольный треугольник. Откуда высота боковой грани пирамиды равна:
h = r / sin φ
Длину радиуса вписанной окружности найдем как
r = S/p
Учитывая, что BC = 2BK, то BC = 2b cos β
откуда
p = ( b + b + 2b cos β ) / 2
p = ( 2b + 2b cos β ) / 2
p = 2b ( 1 + cos β ) / 2
p = b ( 1 + cos β )
Таким образом, радиус вписанной окружности в основание пирамиды будет равен
r = S / p
r = b2sin β cos β / b ( 1 + cos β ) = b sin β cos β / ( 1 + cos β )
Теперь определим высоту боковых граней пирамиды. Зная, что
l / r = cos φ, то
l = r cos φ
Тогда площадь грани пирамиды, прилегающей к равным сторонам основания (а в основании пирамиды у нас лежит равнобедренный треугольник) будет равна:
S1 = lb / 2
S1 = r cos φ * b / 2
S1 = b sin β cos β / ( 1 + cos β ) cos φ * b / 2
S1 = b2 sin β cos β / ( 1 + cos β ) cos φ / 2
S1 = b2 sin β cos β cos φ / ( 2 ( 1 + cos β ) )
Площадь боковой грани, прилегающей к основанию, равна:
S2 = BC * l / 2
S2 = 2b cos β * r cos φ / 2
S2 = b cos β * r cos φ
S2 = b cos β * b sin β cos β / ( 1 + cos β ) * cos φ
S2 = b2 cos2 β sin β cos φ / ( 1 + cos β )
Площадь боковой поверхности пирамиды равна:
Sбок = 2S1 + S2
Sбок = 2 * b2 sin β cos β / ( 2 ( 1 + cos β ) cos φ ) + b2 cos2 β sin β cos φ / ( 1 + cos β )
Sбок = b2 sin β cos β cos φ / ( 1 + cos β ) + b2 cos2 β sin β cos φ / ( 1 + cos β )
Sбок = ( b2 sin β cos β cos φ + b2 cos2 β sin β cos φ ) / ( 1 + cos β )
Sбок = b2 sin β cos β cos φ ( 1 + cos β ) / ( 1 + cos β )
Sбок = b2 sin β cos β cos φ
Откуда площадь полной поверхности пирамиды с равнобедренным треугольником в основании составит:
S = Sбок + Sосн
S = b2 sin β cos β cos φ + b2 cos2 β sin β cos φ / ( 1 + cos β )