∠A = ∠C = 55° и ∠B = ∠D = 125°.
Объяснение:
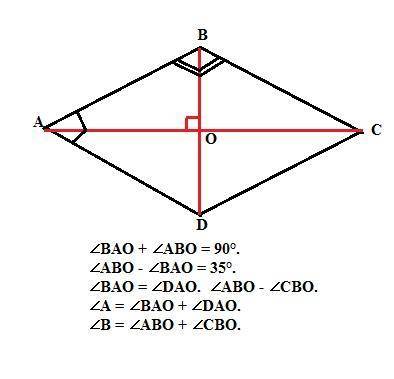
Диагонали ромба взаимно перпендикулярны. Следовательно, они со стороной ромба образуют прямоугольный треугольник. Сумма острых углов прямоугольного треугольника равна 90°, а их разность равна 35° (дано).
Пусть один из углов равен х градусов. Тогда второй равен х+35 градусов.
Значит 2х = 90-35 = 55°. И один из углов треугольника равен 55:2 = 27,5°.
Тогда второй угол равен 27,5+35 = 62,5°.
В ромба диагонали являются биссектрисами его углов. Следовательно, углы ромба равны удвоенным градусным мерам найденных углов прямоугольного треугольника.
Противоположные углы ромба равны.
Углы ромба равны 125° и 55°.
Проверка: углы ромба, прилежащие к одной стороне, в сумме равны 180°.
125+55 = 180°.


Найти: S∆
S∆=½ab
R=c/2 => c=2R
c=2*5=10 см.
r=½(a+b-c)
a+b-c=2r
a+b=2r+c
a+b=2*2+10=14 см
Выразим отсюда катет а
а=14-b
По т. Пифагора
с²=а²+b²
(14-b)²+b²=с²
196-28b+b²+b²=10²
2b²-28b+96=0 |:2
b²-14b+48=0
b1=6 b2=8
Найдем длину катета
а1=14-6=8 см
а2=14-8=6 см
Т.е. один из катетов равен 6 см, другой - 8 см.
S=½•6•8=24 см²