Сумма углов треугольника равна 180°.
В ΔABC:
∠A+∠B+∠C = 180°;
∠B = 180°-(∠A+∠C) = 180°-(60°+40°) = 80°.
Биссектриса делит угол пополам.
∠DBC = ∠ABC:2 = 80°:2 = 40°, как угол при биссектрисе BD.
Если в треугольника два угла равны, то он равнобедренный.
∠DBC = 40° = ∠DCB ⇒ ΔDBC - равнобедренный, ч.т.д.
Стороны треугольника, лежащие напротив равных углов, равны.
В ΔDBC:
сторона BD лежит напротив ∠DCB;
сторона DC лежит напротив ∠DBC;
∠DBC = ∠DCB ⇒ BD = DC.
ответ: BD = DC.
Объяснение:
Наверно , но ты сказал что амне 15дают!
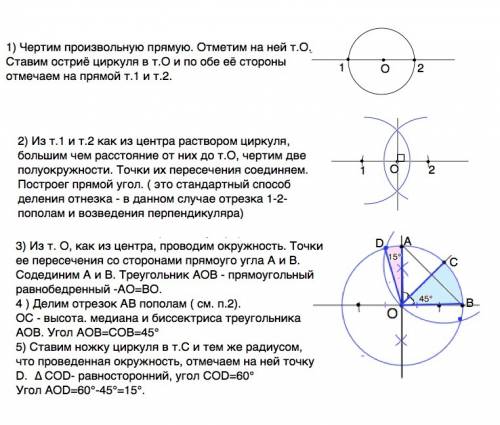
1) Чертим произвольную прямую. Отметим на ней т.О. Ставим остриё циркуля в т.О и по обе её стороны отмечаем на прямой т.1 и т.2.
2) Из т.1 и т.2 как из центра раствором циркуля, большим чем расстояние от них до т.О, чертим две полуокружности. Точки их пересечения соединяем. Построег прямой угол. ( это стандартный деления отнезка - в данном случае отрезка 1-2- пополам и возведения перпендикуляра)
3) Из т. О, как из центра, проводим окружность. Точки ее пересечения со сторонами прямоуго угла А и В.
Содединим А и В. Треугольник АОВ - прямоугольный равнобедренный -АО=ВО.
4 ) Делим отрезок АВ пополам ( см. п.2).
ОС - высота. медиана и биссектриса треугольника АОВ. Угол АОВ=СОВ=45°
5) Ставим ножку циркуля в т.С и тем же радиусом, что проведенная окружность, отмечаем на ней точку D. ∆ СОD- равносторонний, угол СОD=60°
Угол АОD=60°-45°=15°.
Нужные углы построены.
40 градусов ! решение :
найдём угол OAD. BAD = 90 градусов => 90 - 50 = 40 градусов (OAD)
ODA = OAD т.как диагонали равны => треугольник AOD равнобедренный !
180 - (40+40) = 100 ( угол AOD)
теперь берём треугольник EOA . E середина стороны BA. O cередина диагоналей. EO делит треугольник BOA на 2 равных треугольника ! => EO - медиана этого треугольника => угол OEA 90 градусов , 180 - (90+50) = 40 .
EOA+AOD=140 градусов