1. S = 25,5 дм².
2. Cosα = 0,96.
Объяснение:
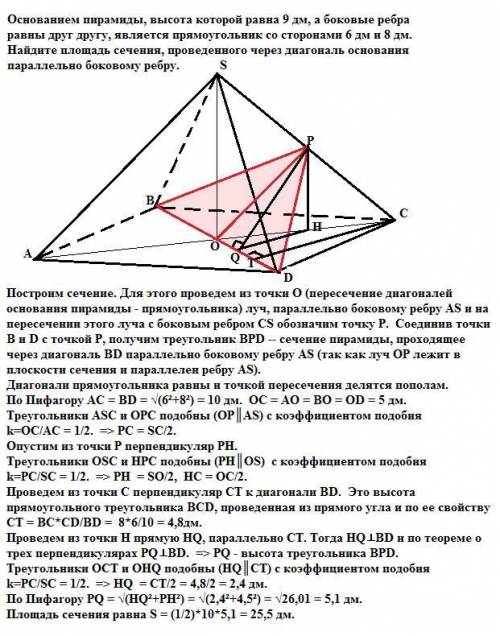
1. Построим сечение. Для этого проведем из точки О (пересечение диагоналей основания пирамиды - прямоугольника) луч, параллельно боковому ребру AS и на пересечении этого луча с боковым ребром CS обозначим точку Р. Соединив точки В и D с точкой Р, получим треугольник BPD -- сечение пирамиды, проходящее через диагональ BD параллельно боковому ребру AS (так как луч ОР лежит в плоскости сечения и параллелен ребру AS).
Диагонали прямоугольника равны и точкой пересечения делятся пополам.
По Пифагору АС = BD = √(6²+8²) = 10 дм. ОС = АО = BO = OD = 5 дм.
Треугольники ASC и OPC подобны (OP║AS) c коэффициентом подобия k=OC/AC = 1/2. => PC = SC/2.
Опустим из точки Р перпендикуляр РН.
Треугольники OSC и HPC подобны (PH║OS) c коэффициентом подобия k=PC/SC = 1/2. => PH = SO/2, НС = ОС/2.
Проведем из точки С перпендикуляр СТ к диагонали BD. Это высота прямоугольного треугольника BCD, проведенная из прямого угла и по ее свойству CТ = BC*CD/BD = 8*6/10 = 4,8дм.
Проведем из точки Н прямую HQ, параллельно СТ. Тогда HQ⊥BD и по теореме о трех перпендикулярах PQ⊥BD и является высотой треугольника BPD.
Треугольники OCТ и OHQ подобны (HQ║CT) c коэффициентом подобия k=PC/SC = 1/2. => HQ = CT/2 = 4,8/2 = 2,4 дм.
По Пифагору PQ = √(HQ²+PH²) = √(2,4²+4,5²) = √26,01 = 5,1 дм.
Площадь сечения равна S = (1/2)*10*5,1 = 25,5 дм².
2. Определение: Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек. АВ1 и СD1 скрещивающиеся прямые по определению.
Угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся.
Проведем диагональ А1В грани АА1В1В. A1B параллельна СD1 как соответствующие диагонали противоположных граней параллелепипеда. АВ1 и А1В - скрещивающиеся прямые. Следовательно, искомый угол - это угол между прямыми АВ1 и А1В. Боковая грань АА1В1В - прямоугольникб диагонали которого пересекаются в точке О и этой точкой делятся пополам. Диагонали равны между собой и по Пифагору равны √(АА1²+АВ²) = √(6²+8²) = 10 ед. Тогда АО = А1О = 5 ед. АА1 = 6 ед. (дано).
Найдем косинус этого угла по теореме косинусов:
Cosα = (AO²+A1O² - AA1²)/(2*AO*AO) = (5²+5²-6²)/(2*25) = 14/50 = 0,28.
Тогда по известной формуле
Sinα = √(1 - Cos²α) = √(0,9216) = 0,96.
1. S = 25,5 дм².
2. Cosα = 0,96.
Объяснение:
1. Построим сечение. Для этого проведем из точки О (пересечение диагоналей основания пирамиды - прямоугольника) луч, параллельно боковому ребру AS и на пересечении этого луча с боковым ребром CS обозначим точку Р. Соединив точки В и D с точкой Р, получим треугольник BPD -- сечение пирамиды, проходящее через диагональ BD параллельно боковому ребру AS (так как луч ОР лежит в плоскости сечения и параллелен ребру AS).
Диагонали прямоугольника равны и точкой пересечения делятся пополам.
По Пифагору АС = BD = √(6²+8²) = 10 дм. ОС = АО = BO = OD = 5 дм.
Треугольники ASC и OPC подобны (OP║AS) c коэффициентом подобия k=OC/AC = 1/2. => PC = SC/2.
Опустим из точки Р перпендикуляр РН.
Треугольники OSC и HPC подобны (PH║OS) c коэффициентом подобия k=PC/SC = 1/2. => PH = SO/2, НС = ОС/2.
Проведем из точки С перпендикуляр СТ к диагонали BD. Это высота прямоугольного треугольника BCD, проведенная из прямого угла и по ее свойству CТ = BC*CD/BD = 8*6/10 = 4,8дм.
Проведем из точки Н прямую HQ, параллельно СТ. Тогда HQ⊥BD и по теореме о трех перпендикулярах PQ⊥BD и является высотой треугольника BPD.
Треугольники OCТ и OHQ подобны (HQ║CT) c коэффициентом подобия k=PC/SC = 1/2. => HQ = CT/2 = 4,8/2 = 2,4 дм.
По Пифагору PQ = √(HQ²+PH²) = √(2,4²+4,5²) = √26,01 = 5,1 дм.
Площадь сечения равна S = (1/2)*10*5,1 = 25,5 дм².
2. Определение: Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек. АВ1 и СD1 скрещивающиеся прямые по определению.
Угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся.
Проведем диагональ А1В грани АА1В1В. A1B параллельна СD1 как соответствующие диагонали противоположных граней параллелепипеда. АВ1 и А1В - скрещивающиеся прямые. Следовательно, искомый угол - это угол между прямыми АВ1 и А1В. Боковая грань АА1В1В - прямоугольникб диагонали которого пересекаются в точке О и этой точкой делятся пополам. Диагонали равны между собой и по Пифагору равны √(АА1²+АВ²) = √(6²+8²) = 10 ед. Тогда АО = А1О = 5 ед. АА1 = 6 ед. (дано).
Найдем косинус этого угла по теореме косинусов:
Cosα = (AO²+A1O² - AA1²)/(2*AO*AO) = (5²+5²-6²)/(2*25) = 14/50 = 0,28.
Тогда по известной формуле
Sinα = √(1 - Cos²α) = √(0,9216) = 0,96.

1) найдем сторону аb по теореме Пифагора :
2 2 2
pb = pa + ab
2 2 2 2
ab = корень (pb - pa ) = корень (17 - 8 ) = 15
2) найдем сторону ас по теореме Пифагора :
2 2 2 2
ас = корень ( pc - pa ) = корень (4корень13 - 8 ) = корень ( 16 * 13 - 64) = 12
3) найдем сторону cb по теореме Пифагора :
2 2 2 2
cb = корень (ab - ac ) = корень (15 - 12 ) = 9
4) Площадь прямоугольного треугольника = 1/2 произведений катетов найдем площади трех прямоугольних треугольников:
Sapb = 1/2 (pa * ab) = 1/2(8*15) = 60
Sapc = 1/2 (ap * ac) = 1/2(8*12) = 48
Sacb =1/2 (ac * cb) = 1/2(12*9)=54
найдем площадь треугольника Spcb = 1/2(pc * cb) = 1/2 (4корень13 * 9)
найдем площадь пирамиды Sapb + Sapc + Sacb + Spcb = 60 + 48 + 54 + 1/2(4корень13*9)