Проекция наклонной на плоскость - это отрезок один из концов которого есть один из концов наклонной принадлежащий данной плоскости, другой - перпендикуляр, опущенный из второго конца наклонной на данную плоскость. Рассмотрим треугольник, образованный наклонной, ее проекцией и перпендикуляром опущенным из конца наклонной не принадлежащего данной плоскости на эту плоскость. Он прямоугольный. Если катет вдвое меньше гипотенузы, то угол противолежащий катету равен 30 градусов, следовательно угол фи равен 180 - (90+30)=60
а) BC1 || AD1, поэтому угол между прямыми AB1 и BC1 равен углу между AB1 и AD1.
ребро куба равно а, поэтому (так как грани куба - квадраты), то AB1=AD1=B1D1, а значит треугольник AB1D1 - правильный(равносторонний),
углы равностороннего треугольника равны 60 градусов,
значит искомый угол между прямыми AB1 и BC1 равен 60 градусов
б) так как В1С1 - перпендикуляр с точки С1 на грань АА1В1В, то угол между прямой AC1 и гранью AA1B1B равен углу В1АС1
(треугольник АВ1С1 - прямоугольным с прямым углом АВ1С1)
по свойству диагонали квадрата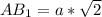
по свойству диагонали куба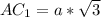
угол В1АС1 равен arccos корень(2/3)т.е.
угол между прямой AC1 и гранью AA1B1B равен arccos корень(2/3) градусов