∠АВС = 80°.
Объяснение:
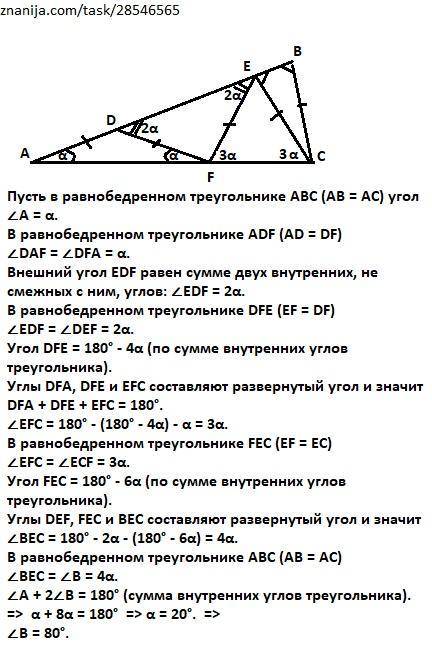
Пусть в равнобедренном треугольнике АВС (АВ = АС) угол
∠А = α.
В равнобедренном треугольнике ADF (AD = DF)
∠DAF = ∠DFA = α.
Внешний угол EDF равен сумме двух внутренних, не смежных с ним, углов: ∠EDF = 2α.
В равнобедренном треугольнике DFЕ (EF = DF)
∠EDF = ∠DEF = 2α.
Угол DFE = 180° - 4α (по сумме внутренних углов треугольника).
Углы DFA, DFE и EFС составляют развернутый угол и значит
DFA + DFE + EFС = 180°.
∠EFC = 180° - (180° - 4α) - α = 3α.
В равнобедренном треугольнике FЕС (EF = ЕС)
∠EFС = ∠EСF = 3α.
Угол FEС = 180° - 6α (по сумме внутренних углов треугольника).
Углы DЕF, FEC и BEC составляют развернутый угол и значит
∠ВЕС = 180° - 2α - (180° - 6α) = 4α.
В равнобедренном треугольнике АВС (АВ = АС)
∠ВЕС = ∠В = 4α.
∠А + 2∠В = 180° (сумма внутренних углов треугольника). => α + 8α = 180° => α = 20°. =>
∠В = 80°.
∠АВС = 80°.
Объяснение:
Пусть в равнобедренном треугольнике АВС (АВ = АС) угол
∠А = α.
В равнобедренном треугольнике ADF (AD = DF)
∠DAF = ∠DFA = α.
Внешний угол EDF равен сумме двух внутренних, не смежных с ним, углов: ∠EDF = 2α.
В равнобедренном треугольнике DFЕ (EF = DF)
∠EDF = ∠DEF = 2α.
Угол DFE = 180° - 4α (по сумме внутренних углов треугольника).
Углы DFA, DFE и EFС составляют развернутый угол и значит
DFA + DFE + EFС = 180°.
∠EFC = 180° - (180° - 4α) - α = 3α.
В равнобедренном треугольнике FЕС (EF = ЕС)
∠EFС = ∠EСF = 3α.
Угол FEС = 180° - 6α (по сумме внутренних углов треугольника).
Углы DЕF, FEC и BEC составляют развернутый угол и значит
∠ВЕС = 180° - 2α - (180° - 6α) = 4α.
В равнобедренном треугольнике АВС (АВ = АС)
∠ВЕС = ∠В = 4α.
∠А + 2∠В = 180° (сумма внутренних углов треугольника). => α + 8α = 180° => α = 20°. =>
∠В = 80°.

512√3 см²
Объяснение:
Выполним рисунок. Дан ромб АБСД, диагональ АС=32√3, диагональ ВД, т.О - точка пересечения диагоналей.
Площадь ромба равна половине произведения его диагоналей. Значит, найдём его диагонали.
1 вариант решения
Рассмотрим ΔАВД.
Он - равносторонний.
Докажем это утверждение. АВ=АД как стороны ромба, значит ΔАВД-равнобедренный с основанием ВД и равными ∠АВД=∠АДВ.
∠АВД=60°, т.к. диагональ ромба ВД, является также и бисектрисой ∠АВС=120°. Сумма внутренних углов треугольника равна 180°, значит ΔДАВ=180-60-60=60°. Все три угла равны, значит доказано, что ΔАВД - равносторонний.
Тогда ВД=АВ=АД.
Т.к. у ромба все стороны равны и их 4, то длина стороны ромба равна периметру ромба, делённому на 4: 128/4=32 см.
Тогда площадь ромба АВСД: АС*ВД/2 = 32√3 * 32 / 2 = 512√3 см².
2 вариант решения.
Рассмотрим ΔАВО.
Он - прямоугольный с
гипотенузой АВ, равной стороне ромба,
∠ВОА=90° т.к. диагонали ромба пересекаются под прямым углом
и катетами АО и ВО, равными соответственно половинам диагоналей АС и ВД, т.к диагонали ромба точкой пересечения делятся пополам,
∠АВО=60°, т.к. диагональ ромба ВД, является также и бисектрисой ∠АВС=120°.
Найдём ВО. Эту величину можно найти 2-мя путями.
ВО=АВ*cos∠ABO = Р/4 * cos 60° = 32 * 0.5 = 16 см или
ВО=АО*ctg∠ABO = 16√3 * 1/√3 = 16 см.
Тогда площадь ромба АВСД: АС*ВД/2 = 32√3 * 16 * 2 / 2 = 512√3 см².
Наличие такого количества решений возникло по причине избыточности условия. Эту задачу можно было бы решить не зная величины периметра ромба, либо без длины диагонали. Ключевое условие здесь, это значение угла , равное 120°.