В основании правильный четырёхугольник значит это квадрат, и диагональ в нём -биссектриса. Обозначим пирамиду АВСДМ. Где М вершина.Проведём высоту пирамиды МО она приходит в центр располагаясь на диагонали АС. Известно АС=а*корень из2. Где а сторона основания то есть а* корень из2=10. Отсюда а=АД=5корней из 2. Проведём из точки О перпендикуляр к АД в точку Е. Соединим точки М и Е. МЕ- апофема. Найдём ОЕ=корень из(АОквадрат -АЕ квадрат)=корень из 12,5. По теореме Пифагора находим МЕ=корень из(МОквадрат+ОЕ квадрат)=корень из(144-12,5)=12,5
Відповідь: 1) 16√21 см; 2) 135 см²
Пояснення:
1) P ромба=4АВ, тому AB=P/4=40/4=10 см
Позначу точку О перетину взаємно перпендикулярних діагоналей. Вона ділить їх навпіл, тобто АО=ОС=АС/2=8/2=4 см
∆АОВ, <АОВ=90°, за теоремою Піфагора ОВ=√(АВ²-АО²)=√(10²-4²)=√(100-16)=√84=2√21 см
ВD=2OB=2√21×2=4√21 см
S ромба=0,5d1d2=0,5AC×BD=0,5×8×4√21=16√21 см²
2) Дано прямокутник ABCD. Нехай х - коефіцієнт пропорційності, тоді AB=3x, BC=5x.
P=2(AB+BC)
2(3x+5x)=48
8x=24, x=3
AB=3x=3×3=9 см, BC=5х=3×5=15 см
S=AB×BC=9×15=135 см²
Два возможных случая:
1) 
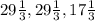
2) 
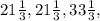
Объяснение:
Т.к. треугольник равнобедренный, то по определению имеет 2 равные боковые стороны.
Случай 1. Пусть основание меньше боковой стороны, тогда основание = x, а боковые стороны x + 12. Периметр - это сумма всех сторон, так что составим уравнение:
x + (x+12) + (x+12) = 76
3x + 24 = 76
3x = 76 -24
3x = 52
x = 52: 3 =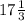 
- основание, значит боковая сторона = x + 12 =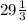 
Случай 2. Пусть основание больше боковой стороны, тогда основание = x, а боковые стороны x - 12.
Составляем уравнение
x + (x-12) + (x-12) = 76
3x - 24 = 76
3x = 76 + 24
3x = 100
x = 100:3 =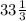 
, ⇒ боковая сторона = x - 12 =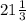 
если пирамида правильная..то..через теорему пифагора можно найти ребро пирамиды..высота - катет , 10/2 - катет..отсюда ребро равно 13..далее найдем сторону квадрата..по диагонали(биссектрисе)..и отсюда снова через теорему пифагора : у нас ребро - гипотенуза..сторона квадрата есть..делим ее пополам возводим в квадрат отнимаем от гипотенузы..и получаем апофему