0,5 мм
Объяснение:
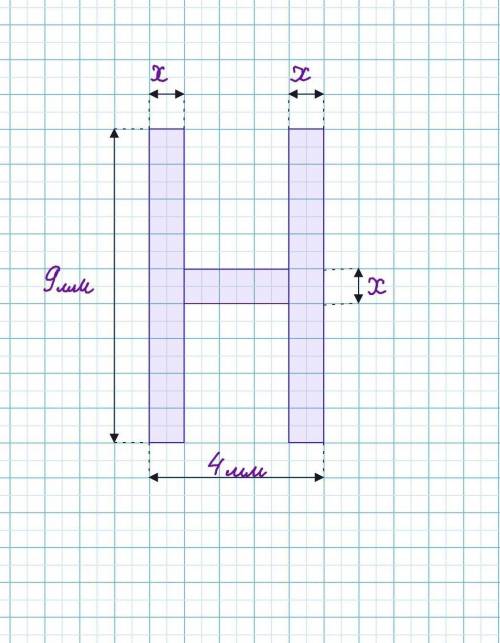
Пусть толщина буквы - х мм.
Буква Н состоит из трёх прямоугольников: двух одинаковых вертикально расположенных и одного горизонтально расположенного.
Площадь прямоугольника вычисляется по формуле: S=a×b, где а - длина, b - ширина.Тогда площадь вертикально расположенных прямоугольников : по 9х мм² каждый.
Площадь горизонтально расположенного прямоугольника: (4-2х)×х мм².
Так как площадь буквы составляет 10,5 мм², составляем уравнение:
9х+9х+(4-2х)×х=10,5
18х+4х-2х²-10,5=0
-2х²+22х-10,5=0
х²-11х+5,25=0
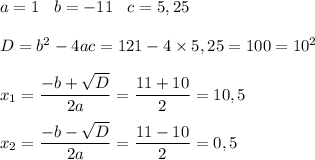
Получили, что толщина буквы равна 0,5 мм либо 10,5 мм.
10,5 мм не подходит по условию, т.к. в этом случае ширина и длина самой буквы будет больше, чем 4мм и 9мм соответственно.
ответ: толщина буквы 0,5 мм
1) <C = 180° - 100° = 80°.
2) <A = 180° - 40° - 80° = 60°
ответ: <A = 60°.
Рис.21) <A = 180° - 150° = 30°
2) <C = 180° - 90° = 90°
3) <B = 180° - 30° - 90° = 60°
ответ: <A = 30°, <B = 60°
Рис.31) <B = 40° , т.к. углы вертикальные
2) <C = 180° - 120° = 60°
3) <A = 180° - 40° - 60° = 80°.
ответ: <A = 80°, <B = 40°
Рис.41) <B = 180° - 140° = 40°
2) <A = <C = (180-40):2 = 70°, т.к. тр. ABC равнобедренный, а в нем углы при основании равны.
ответ: <A = <C = 70°
a = 8 см - длина основания
c = 10 см - диагональ
h = 10 см - высота
По теореме Пифагора находим вторую сторону.
b = √10² - 8² = √36 = 6 см - ширина
Площадь боковой поверхности
Sбок = 2*(a+b)*h = 2*(8+6)*10 = 280 см² - боковая
Sосн = a*b = 8*6 = 48 см² - основание
Sполн = 280 + 2*48 = 376 см² - площадь полной поверхности - ОТВЕТ