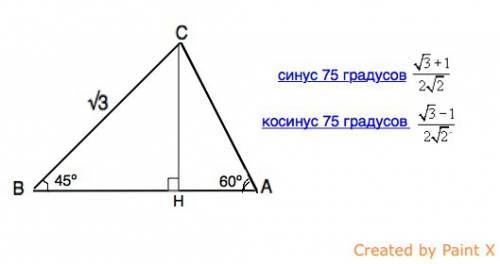
Решением треугольника называется нахождение всех его шести элементов (т. е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Из суммы углов треугольника найдем угол С:
∠С=180º-45º-60º=75º
В прямоугольном ⊿ ВНС угол ВСН=90º-45º=45º
⊿ ВНС - равнобедренный, СН=ВН=ВС•sin 45º=(√3•√2):2
В ⊿ АНС сторона АС=СH:sin 60º
AC=[(√3•√2):2]:(√2):2=√2
АВ=ВН+АН
АН противолежит углу НСА, равному 90º-60º=30º
АН=АС:2=(√2):2
АВ=(√3•√2):2+(√2):2=(√3+1):√2
––––––––––––
Или по т. синусов:
АВ:sin75=BC:sin60
sin 60º=(√3):2
sin 75º=(√3+1):2√2 ( из таблицы тригонометрических функций)
АВ:(√3+1):2√2=(√3):[(√3):2]⇒
AB=(√3+1):√2
--------------
или по т.косинусов
AB²=BC²+AC²- 2BC•AC•cos75º
cos 75º=(√3-1):2√2
AB²=3+2- 2√6•((√3-1):2√2)⇒
AB=√(2+√3)
Оба найденных значения АВ равны - проверьте, возведя их в квадрат.
[√(2+√3)]²=[(√3+1):√2]²
57° и 33°.
Объяснение:
1) При пересечении диагоналей прямоугольника образовалось 2 пары равных углов:
2 угла - по 66 градусов,
и 2 угла по 180-66 = 114 градусов.
2) Все 4 образовавшихся треугольника являются равнобедренными, так как диагонали прямоугольника равны и в точке пересечения делятся пополам.
3) Следовательно в треугольнике, у которого угол при вершине равен 66°, углы при основании равны:
(180 - 66) : 2 = 114 : 2 = 57° - это первый угол, который диагональ образует со стороной прямоугольника.
4) Находим второй угол. Для этого от 90° (так как у прямоугольника углы прямые) отнимаем 57°:
90 - 57 = 33°.
ПРОВЕРИМ полученные значения по другому треугольнику, у которого угол при вершине равен 114°.
Углы при основании:
(180 - 114): 2 = 66 : 2 = 33°
Вторые углы:
90 - 33 = 57°.
Получили те же самые значения:
57° - больший угол;
33° - меньший угол.
ответ: 57° и 33°.