Данные точки лежат на поверхности шара, следовательно, не лежат на одной прямой.
Через любые три точки пространства, не лежащие на одной прямой, можно провести одну и только одну плоскость. Относительно к шару эта плоскость будет сечением, а сечение шара - круг.
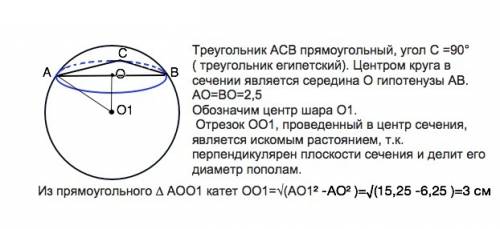
Соединив данные точки, получим треугольник АСВ, причем угол С =90° ( треугольник египетский). Тогда центром круга в сечении является середина О гипотенузы АВ.
r=АО=ВО=2,5
Обозначим центр шара О1.
Отрезок, проведенный в центр сечения, является искомым расстоянием, т.к. перпендикулярен плоскости сечения и делит его диаметр пополам.
Из прямоугольного ∆ АОО1 катет
ОО1=√(AО1² -АО² )=√(15,25 -6,25 )=√9=3 см
№1.
Угол между касательной и радиусом, проведенным к ней равен 90 градусов, поэтому ОА будет гипотенузой в треугольнике АВО, а ОВ - катетом. Дальше из теоремы Пифагора:
АВ=
и того, АВ=8
ответ:8см.
№2.
уголA+уголB+уголC=180°( по теореме о сумме углов в треугольнике)
Уравнение:
Пусть Х будет угол А, тогда 3Х угол В, а 5Х угол С
Х+3Х+5Х=180
9Х=180
Х=180:9
Х=20°
20*3 равно=60градусов
ответ: угол В= 60 градусов, угол С= 100 градусов.
№3.
Длина диаметра 20 см. Концы диаметра и данная точка окружности образуют вписанный угол, опирающийся на диаметр. Вписанный угол, опирающийся на диаметр, прямой.
Значит, получившейся треугольник будет прямоугольным. Расстояние от другого конца диаметра до данной точки найдем по теореме Пифагора, как длину катета прямоугольного треугольника:
=(20-16)(20+16)=4*36=144
см
ответ:12 см.
идеально
Объяснение:
Доказать: ΔМКО = ΔРНО
Доказательство: Т.к. ∠МОК=∠РОН, как вертикальные углы, то треугольники МОК и РОН равны по стороне и двум прилежащим к ней углам (∠МКО = ∠РНО, НО=ОК по условию)