ВС перпендикулярен плоскости, следовательно, перпендикулярен любой прямой, лежащей в этой плоскости и проходящей через его основание С. ⇒ ∆ ВСА - прямоугольный с прямым углом С.
По т.о 3-х перпендикулярах: если наклонная перпендикулярна прямой, лежащей в плоскости, значит, этой прямой перпендикулярна и ее проекция.
ВА - перпендикулярен ребру МК двугранного угла, следовательно его проекция СА перпендикулярна прямой МК.
Величиной двугранного угла является градусная мера его линейного угла.
Линейный угол двугранного угла – угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
АВ и АС перпендикулярны МК. Следовательно, угол ВАC -искомый.
ctg BAC =2:2√3=1/√3 - это котангенс 60°.
Угол ВАС=60°
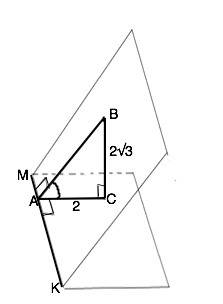
ВС перпендикулярен плоскости, следовательно, перпендикулярен любой прямой, лежащей в этой плоскости и проходящей через его основание С. ⇒ ∆ ВСА - прямоугольный с прямым углом С.
По т.о 3-х перпендикулярах: если наклонная перпендикулярна прямой, лежащей в плоскости, значит, этой прямой перпендикулярна и ее проекция.
ВА - перпендикулярен ребру МК двугранного угла, следовательно его проекция СА перпендикулярна прямой МК.
Величиной двугранного угла является градусная мера его линейного угла.
Линейный угол двугранного угла – угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
АВ и АС перпендикулярны МК. Следовательно, угол ВАC -искомый.
ctg BAC =2:2√3=1/√3 - это котангенс 60°.
Угол ВАС=60°

Для начала найдем боковую сторону трапеции
AB1=(AD-BC)/2=(10-6)/2=2
AB=AB1/sin30=2*2=4
Надо найти высоту BB1^2=AB^2-AB1^2=16-4=12
BB1==2√3
решим без интегралов, вся площадь поверхности состоит из 3 частей, 2 одинаковых конусообразных поверхностей S1 снизу и сверху и цилиндрической посередине S2
S2=2pi*BB1*BC=2*2√3*6*pi=24√3 pi
S1=pi*BB1*AB=pi*2√3*4=8√3pi
Тогда общая площадь поверхности
S=2S1+S2=2*8√3pi+24√3pi=40√3pi