Противолежащие стороны параллелограмма равны (из свойства фигуры параллелограмм).
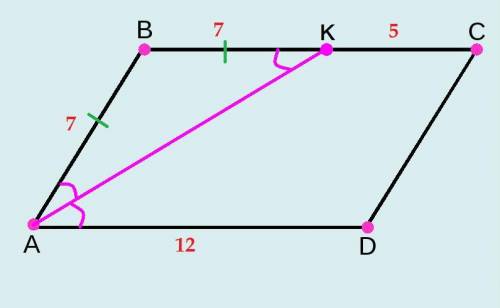
=> BC=AD=12 (см) => BK=12-5=7 (см).
Так как АК - биссектриса (по условию), то она делит угол А так, что углы ВАК и КАD равны между собой.
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны (из определения).
=> при пересечении двух параллельных прямых секущей накрест лежащие углы равны.
=> угол ВКА = углу КАD, а они накрест лежащие при ВС || АD и секущей АК.
В равнобедренном треугольнике две боковые стороны равны и углы при основании тоже равны (из свойства равнобедренного треугольника).
=> треугольник АВК - равнобедренный (угол ВАК = углу ВКА) и АВ=ВК=7 (см).
Периметр параллелограмма равен удвоенной сумме 2х его соседних сторон (из теоремы о периметре параллелограмма).
=> Р=2*AB+2*AD=2*7+2*12=14+24=38 (см).
ответ: Р параллелограмма АВСD равен 38 (см).
ответ: треугольнике АВС угол АСВ опирается на диаметр АВ, следовательно его величина равна 900, а треугольник АВС прямоугольный.
По условию, СМ перпендикулярно АВ, тогда отрезок СН - высота СН треугольника АВС. В прямоугольном треугольнике АСН катет СН лежит против угла 300, а следовательно равен половине длины гипотенузы АС.
СН = АС / 2 = 8 / 2 = 4 см.
Диаметр окружности АВ делит хорду СМ пополам, так как они перпендикулярны, тогда длина хорды СМ = 2 * СН = 2 * 4 = 8 см.
ответ: Длина хорды СМ равна 8 см.
Объяснение:
∠AOB = 60°- между диагоналями.
AB = 6√3 - ширина прямоугольника
НАЙТИ
BC = ? - длину
РЕШЕНИЕ
Рисунок к задаче - в приложении.
ΔABO - равносторонний - все углы равны 60°
∠OBC = 90-60 = 30°
BO= AB = 6*√3
BE=BO*cos30° = 6√3* 1/2*√3= 6*3/2 = 9
a = 2* BE = 2*9 = 18 - длина - ОТВЕТ