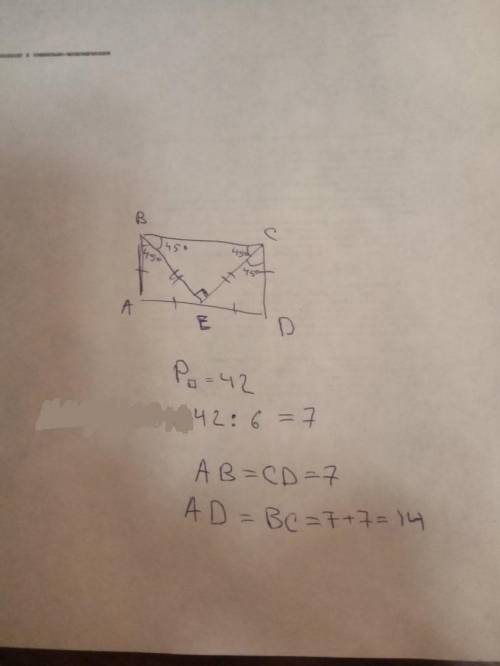
ответ: АВ=CD=7 AD=BC=14
Объяснение: назовем точку снизу как Е. треугольник ВЕС будет равнобедренным и прямоугольным, т.к. точка Е делит сторону АD пополам. Следовательно катеты треугольника будут равны и углы EBC и ECB будут равны 45 градусам. Далее следует что углы АВЕ, ECD, ВЕА и CED будут равны 45 градусам, и отсюда следует, что треугольники ABE и ECD так же равнобедренные и прямоугольные. Отсюда следует, что AB=AE=ED=CD, а сторона ВС = AD и BC = АЕ+ЕD.
Далее делим 42 на 6 = 7 (стороны АВ и CD)
а стороны AD и BC будут равны 7+7 = 14 , так как АЕ=ЕD

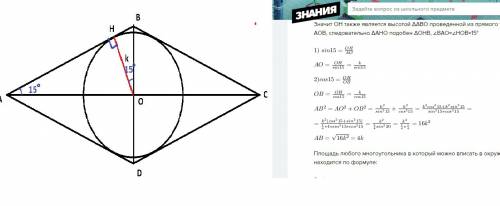
Поскольку центр описанной окружности лежит на основании трапеции,
это основание - диаметр окружности и гипотенуза треугольника, где
боковая сторона и диагональ - катеты, а большее основание трапеции - гипотенуза. Меньший угол между диагоналями 80°,
больший, как смежный с ним, равен 100°.
В треугольнике АОД углы при основании АД равны половине разности между суммой всех его углов и углом при вершине:
∠ОАД=∠ОДА=(180°-100°):2=40°
В ⊿ АСД один из острых углов равен 40°, второй
∠АДС=180°- 90°- 40°=50°
Сумма углов при боковой стороне трапеции равна 180°
Следовательно, если острый угол трапеции равен 50°, то тупой ∠АВС=180°-50°=130°