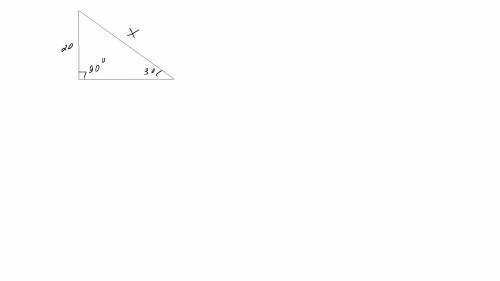
4) по теореме синусов получаем извняюсь перепутал
x/sin90=20/sin30
x=40
ответ 40 см
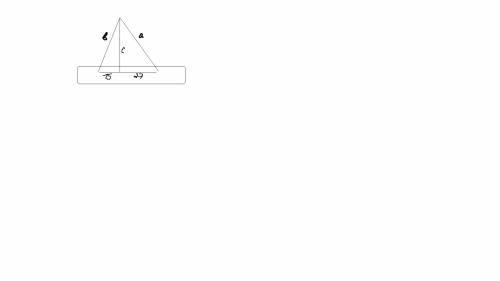
5(1) пусть Сторона равняються а и в
тогда
{a-b=6
{b^2-a^2=15^2-27^2
{a=6+b
{b^2-(36+12b+b^2)=-504
{b^2-36-12b-b^2=-504
{ -12b=-504+36
{b=39
{a=45
Значит сама длина равняеться C=V39^2-225=V1296=36
ответ длина равняеться 36см
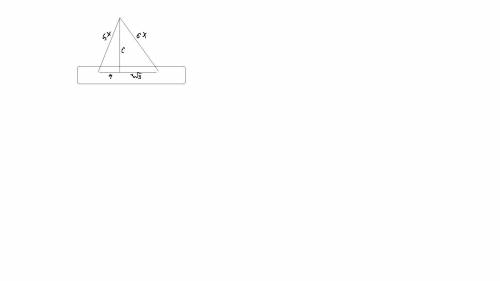
5(2)
пусть первая сторона 5х тогда вторая 6х
По теореме Пифагор
36x^2-27=25x^2-16
11x^2=11
x=1
Значит длина равняеться 5^2-4^4=3^2
ответ длина равняеться 3см
6) щас решу
2x^2=256
x=8V2
Половина
y=V128-64=8
y2=V17^2-8^2=15
искомая равна =V(8^2+15^2-2*8*15cos60)=13
Уравнение сферы с центром в точке (x0; y0; z0) и радиусом R записывантся так
(X-x0)^2 + (Y-y0)^2 + (Z-z0)^2 = R^2
нам неизвестны x0; y0; z0 и R и у нас есть 4 точки через которые проходим сфера
подставляя координатв этих точек в уравнение получим 4 уравнения
А(2;-5;8) ===> (2-x0)^2 + (-5-y0)^2 + (8-z0)^2 = R^2
В(8;-2;5) ===> (8-x0)^2 + (-2-y0)^2 + (5-z0)^2 = R^2
С(5;-8:2)) ===> (5-x0)^2 + (-8-y0)^2 + (2-z0)^2 = R^2
Д(-2;-8;-5) ===> (-2-x0)^2 + (-8-y0)^2 + (-5-z0)^2 = R^2
подставим R^2 из последнего в первые 3
(2-x0)^2 + (-5-y0)^2 + (8-z0)^2 = (-2-x0)^2 + (-8-y0)^2 + (-5-z0)^2
(8-x0)^2 + (-2-y0)^2 + (5-z0)^2 = (-2-x0)^2 + (-8-y0)^2 + (-5-z0)^2
(5-x0)^2 + (-8-y0)^2 + (2-z0)^2 = (-2-x0)^2 + (-8-y0)^2 + (-5-z0)^2
переносим нелево и разкладываем как разность квадратов
(2-x0)^2 -(-2-x0)^2 = ((2-x0) - (-2-x0)) * ((2-x0) + (-2-x0)) = 4*(-2x0) = -8x0
(-5-y0)^2 - (-8-y0)^2 = ((-5-y0) - (-8-y0)) * ((-5-y0) + (-8-y0)) =3*(-13-2y0) =-39 -6y0
(8-z0)^2 - (-5-z0)^2= ((8-z0) - (-5-z0)) * ((8-z0) + (-5-z0)) = 13*(3-2z0) = 39 - 26z0
первое уравнение станет таким
-8x0 + (-39 -6y0) + (39 - 26z0) = -8x0 -6y0 - 26z0 =0
(8-x0)^2 - (-2-x0)^2 = ((8-x0) - (-2-x0)) * ((8-x0) + (-2-x0)) =10*(6-2x0) = 60 - 20x0
(-2-y0)^2 -(-8-y0)^2 = ((-2-y0) - (-8-y0)) * ((-2-y0) + (-8-y0)) = 6*(-10-2y0) = -60 -12y0
(5-z0)^2 - (-5-z0)^2 = ((5-z0) - (-5-z0)) * ((5-z0) + (-5-z0)) =10*(-2z0) = -20z0
второе уравнение станет таким
60 - 20x0 + (-60 -12y0) + (-20z0) = -20x0 -12y0 - 20z0 =0
(5-x0)^2 - (-2-x0)^2 = ((5-x0) - (-2-x0)) * ((5-x0) + (-2-x0)) = 9*(3-2x0) = 27 - 18x0
(-8-y0)^2 - (-8-y0)^2 = ((-8-y0) - (-8-y0)) * ((-8-y0) + (-8-y0)) = 0*(-16-2y0) = 0
(2-z0)^2 - (-5-z0)^2 = ((2-z0) - (-5-z0)) * ((2-z0) + (-5-z0)) = 7*(-3-2z0) = -21-14z0
третье уравнение станет таким
27 - 18x0 + (-21-*14z0) = -18x0 + 0 - 14z0 +6 =0
получили 3 уравнения
-8x0 - 6y0 - 26z0 =0
-20x0 -12y0 - 20z0 =0
-18x0 + 0 - 14z0 = -6
возмем 1первое и умножим на 2 и вычтем из него второе уравнение получим
-16x0+20x0 -12y0+12y0 -52z0+20z0 =0 ==> 4x0 - 32z0 =0
припишем 3 уравнение > -18x0 - 14z0 = -6
первое их написанных умножим на 9 , а второе на 2 и сложим
9*4x0 - 2*18x0 - 9*32z0 - 2*14z0 = -12 ==> (-288-28)z0=-12 ==> z0=12/316=3/79
4x0 - 32z0 =0 ==> 4x0 = 32z0 =32*3/79 ==> x0 = 32*3/79/4 =8*3/79=24/79
-8x0 -6y0 - 26z0 =0 ==> 6y0 =-8x0 - 26z0 = -8*24/79 - 26*3/79 = (-192-78)/79=-270/79 ==> y0 =-270/79/6 =-45/79 = R^2 = (2-x0)^2 + (-5-y0)^2 + (8-z0)^2 подставть найденные значения и найдешь R
Δ AMC и Δ CMB - равнобедренные (AM=MC, MC=MB соответственно).
Углы при основании данных треугольников будут равны. В Δ AMC ∠MAC=∠MCA, а в Δ CMB ∠MCB=∠MBC. ⇒ ∠MAC=∠MCA=∠MCB=∠MBC.
Пусть x - градусная мера каждого угла.
x+x+2x=180°
4x=180°
x=45°
∠A=45°
∠B=45°
∠C=∠MCA+∠MCB=90°