Впараллелограмме abcd диагональ ac со сторонами ab и bc образует углы, равные соответственно 40 и 35. чему равна величина угла c

👇

Ответ:

Elenawow

14.03.2021

Итак. <ВАС=35*
<АВС=40*
Диагональ, проведённая из вершины параллелограмма делит его на 2 равных треугольника.
(Ну или можно так: <АВС=<СDA по трём сторонам)
У равных треугольников соответственные углы равны, т.е.:
ВАС=АDC=35*
рассмотрим треугольник АВС:
180-40-35=105*
105+35=140*

(я мог допустить ошибку, так что лучше перепроверить)

4,8(24 оценок)

Открыть все ответы

Ответ:

myzroman

14.03.2021

В начале построим рисунок, который приложу вложением. Для наглядности соединим т. О поочерёдно с точками A, B, C, D. Получаем пирамиду с вершиной в т. O, в основании которой лежит квадрат ABCD.
Первый вопрос: 1). Докажем, что плоскость ABCD параллельна плоскости A1B1C1D1. Для этого построим пары диагоналей AC, BD, а также A1C1, B1D1.
2). Теперь рассмотрим треугольник OBD. Прямая B1D1 параллельна прямой BD, как средняя линия треугольника OBD, т.к. B1D1 соединяет середины его сторон B1 и D1 (эти точки середины по условию).
3). Теперь рассмотрим треугольник OAC. Прямая A1C1 параллельна прямой AC, как средняя линия треугольника OAC, т.к. A1C1 соединяет середины его сторон A1 и C1 (эти точки середины по условию).
4). Тогда получаем, что две пересекающиеся прямые AC и BD плоскости ABCD параллельны двум пересекающимся прямым A1C1 и B1D1 плоскости A1B1C1D1, а из этого, по теореме о параллельности двух плоскостей, следует, что плоскости ABCD и A1B1C1D1 параллельны, что и требовалось доказать.
Второй вопрос: 1). Рассмотрим треугольник OBA. B1A1 - средняя линия треугольника OBA, т.к. соединяет середины сторон OB и OA (B1 и D1 середины по условию). Тогда B1A1=1/2 AB=10/2=5.
2). Аналогично B1C1 - средняя линия треугольника BC, C1D1 - средняя линия треугольника CD, A1D1 - средняя линия треугольника AD.
3). Тогда, B1C1=5, C1D1=5, A1D1=5.
4). Периметр A1B1C1D1=B1C1+C1D1+A1D1+B1A1=5+5+5+5=20

Квадраь abcd со стороной 10 см и точка o не лежат в одной плоскости точки a1b1c1d1 являются середина

Квадраь abcd со стороной 10 см и точка o не лежат в одной плоскости точки a1b1c1d1 являются середина

4,6(50 оценок)

Ответ:

MilenaSmail12

14.03.2021

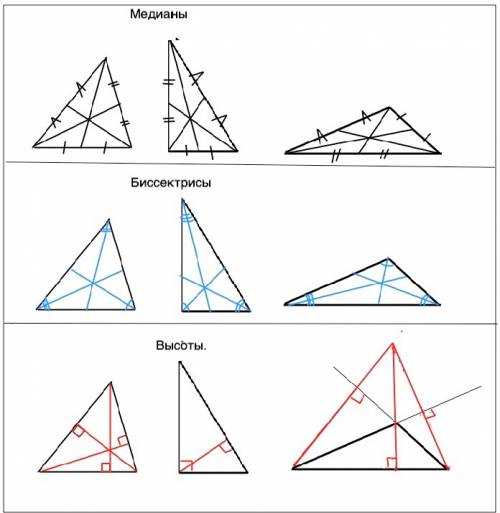
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.

Биссектрисы треугольника пересекаются в одной точке, расстояние от которой до сторон треугольника одинаково и является центром вписанной окружности.

Высоты треугольника пересекаются в одной точке. Точка пересечения высот остроугольного треугольника находится внутри него. Точка пересечения высот прямоугольного треугольника - вершина прямого угла.

Высоты тупоугольного треугольника, проведенные из вершин его острых углов, проходят вне его и пересекают продолжения сторон. Точка пересечения высот тупоугольного треугольника находится вне треугольника.