66 см²
Объяснение:
Медианы треугольника пересекаются в одной точке, и точкой пересечения делятся в отношении 2:1, считая от вершины.
⇒ ВМ:МК=2:1.
У ΔАМК и ΔАВМ одна и та же высота АН - перпендикуляр, проведенный из вершины А к прямой ВК, содержащей стороны ВМ и МК этих треугольников.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты) ⇒
Samk/Sabm=1/2 ⇒
11/Sabm=1/2 =>
22=Sabm.
Sabk=22см²+11см²=33см²
медиана ВК делит ΔАВС на два равновеликих т.е Sabk = Skbc.
⇒
Sabc=33*2=66см²
13 2/3; 19 2/3; 6√2
Объяснение:
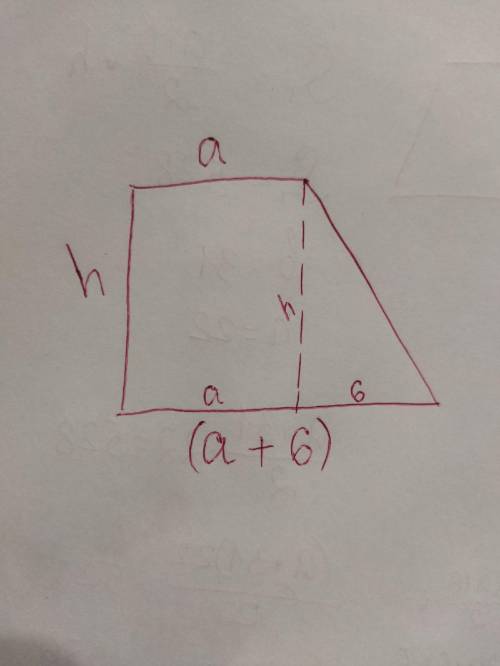
Sтрапеции=(a+b)/2*h
Пусть меньшее основание трапеции равно x, тогда большее основание равно x+6;
Подставляем данные задачи в уравнение
100=(x+x+6)/2*6
100=(2x+6)/2*6
200=(2x+6)*6 (сокращаем на 2)
100=(2x+6)*3
100=6x+18
6x=100-18
6x=82
x=82/6
x=13 2/3
Вычисляем большее основание
13 2/3 + 6 = 41/3 + 6 = 41/3 + 18/3 = 59/3 = 19 2/3
Так как трапеция прямоугольная, мы уже знаем три стороны трапеции, оставшуюся сторону, можно найти через дополнительное построение, получив прямоугольный треугольник и по теореме Пифагора вычислить оставшуюся сторону:
a^2+b^2=c^2
b=h (высоте трапеции) = 6
a=6 (разница между основаниями)
6^2+6^2=36+36=72=6√2
1a,2б,3в второе не знаю , надеюсь