Напишіть рівняння середньої лінії mn трикутника abc і знайдіть її довжину якщо a ( -1 ; -3) b (3; 7) c (5; 1)

👇

Ответ:

vfvf2304

10.04.2020

Дано: ΔABC, A(-1;-3), B(3;7), C(5;1). MN||AC
решение:
средняя линия треугольника параллельна стороне и равна её половине/
длина стороны АС:
$|AC|= \sqrt{( x_{C}- x_{A} ) ^{2}+ ( y_{C}- y_{A} )^{2} } = \sqrt{ (5-(-1))^{2}+ (1-(-3))^{2} } =$
$= \sqrt{ 6^{2}+ 4^{2} } = \sqrt{40} = \sqrt{4*10} =2 \sqrt{10}$
|AC|=2√10
ответ: MN=√10

4,6(16 оценок)

Открыть все ответы

Ответ:

avrora26

10.04.2020

Даны: острый угол А и отрезок СН.

Построить прямоугольный треугольник с углом, равным А, и высотой, равной СН.

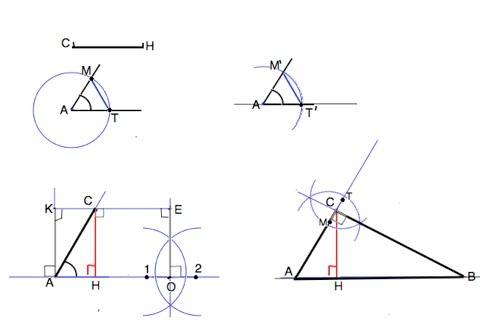
1) Из вершины А данного угла произвольным раствором циркуля делаем насечки М и Т на его сторонах .Соединим МТ.

2) На произвольной прямой а отмечаем т.А и тем же раствором циркуля проводим из нее, как из центра, полуокружность. Точку пересечения полуокружности и прямой обозначим Т'.

3) Циркулемм раствором, равным отрезку ТМ, из точки Т' делаем насечку на полуокружности в т.М' . Проведем прямую через точки А и M'.

Данный угол построен..

4) На прямой а выбираем произвольно точку О, отмечаем по обе стороны от нее на равном расстоянии т.1 и т.2. Из этих точек, как из центров, строим полуокружности так, чтобы они пересеклись по обе стороны от прямой а. Точки их пересечения соединяем прямой. Мы построили общеизвестным прямую, перпендикулярную прямой а

5) Таким же образом восстанавливаем перпендикулярную прямую через т. А. На обеих перпендикулярных прямых отмечаем т.К и т.Е на расстоянии от прямой а, равном длине высоты СН, и соединяем их. Прямая КЕ параллельна прямой АО - её точки находятся на равном расстоянии от а.

6)Точка пересечения КЕ со стороной построенного угла А - вершина С прямого угла искомого треугольника. С циркуля от А откладываем на второй стороне угла расстояние АН=КС.

Соединим С и Н. Высота построена.

По тому же как построены перпендикулярные прямые к т.О и т.А, построим прямой угол в т. С.

7) Прямую, соединяющую точки пересечения полуокружностей, продлим до пересечения с прямой а, и обозначим точку пересечения В. Это вершина второго острого угла искомого треугольника, а АВ - его гипотенуза.

В треугольнике АВС угол САВ равен данному, угол АСВ - прямой по построению, высота СН равна данной. Искомый треугольник построен..

Постройте прямоугольный треугольник по острому углу и высоте проведённый к гипотенузе скиньте фото,

4,6(62 оценок)

Ответ:

vladekan

10.04.2020

Построение ясно из рисунка.
Поскольку плоскость проходит через точки В,С и М, значит она проходит через среднюю линию MN грани АСD, параллельную ребру ВС. Продлим прямые ВМ и СN до их пересечения в точке Р. Треугольник ВРС равнобедренный, следовательно вершина S пирамиды SBPC спроецируется на высоту PF основания ВРС, являющуюся и медианой основания, в точке Н.
Расположение точки Н на прямой PF зависит от угла SQF между плоскостями ВРС и АSВ. В нашем случае этот угол тупой, поэтому точка Н лежит вне грани АSD пирамиды SABCD.

Так как пирамида правильная, в основании - квадрат.
Диагональ квадрата равна в нашем случае 6√2.
Ее половина ОС=3√2.
Высота пирамиды по Пифагору SO=√(SC²-OC²)=√(144-18)=3√14.
Необходимо найти перпендикуляр SH к плоскости BCMN.
Вариант решения - через подобие прямоугольных треугольников SHE и FOE по равным острым углам при вершине Е. Углы SHE и EOF - прямые.
Из этого подобия имеем соотношение: SH/FO=SE/EF и SH=FO*SE/EF.
Высота пирамиды SO=3√14 (по Пифагору из треугольника SOC).
Тогда QG=0,5*SO (так как MN - средняя линия треугольника ASD, и значит QG - средняя линия треугольника KSO).
Из подобия треугольников QGF и EOF имеем ЕО=FO*QG/FG.
FO=3, QG=1,5√14, FG=4,5. Тогда ЕО=3*1,5√14/4,5=√14 и, следовательно, SE=SO-EO=2√14.
EF находим из треугольника EOF по Пифагору:
EF=√(OF²+OE²)=√(9+14)=√23. Тогда SH=3*2√14/√23.
ответ: SH=6√14/√23.

Вправильной четырехугольной пирамиде sabcd основание abcd - квадрат со стороной 6, а боковое ребро р