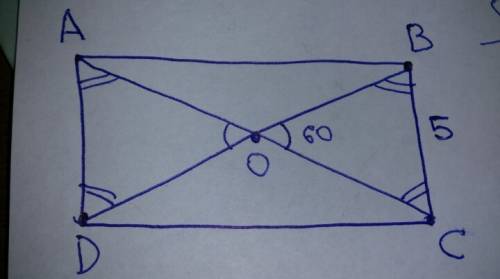
1. В прямоугольнике диагонали образуют треугольники, у которых углы при основании равны.
2. Угол BOC=AOD (как вертикальные); рассмотрим треугольник BOC: угол OBC=OCB, ВС=5 см. Т.к. в треугольнике сумма углов равна 180 градусам, то 180-60=120 гр, а 120:2=60 гр. Значит, OBC=OCB=60 гр., а треугольник BOC - равносторонний.
3. Треугольники BOC и AOD равны, т.к. угол BOC=AOD (как вертикальные), DAO=OCB=ADO=OBC (как внутренне накрест лежащие). BC=AD=BO=OC=AO=DO=5 см.
Значит, диагональ AC=DB (т.к. точка О середина пересечения диагоналей) = 10 см
ответ: AC=DB=10 cv
1) Зависимость площади боковой поверхности S от образующей L;
Косинус половины угла при вершине по теореме косинусов:
cos(α/2) = (R² + L² - R²)/(2RL) = L/2R.
Отсюда синус равен: sin(α/2) = √(1 - (L²/4R²).
Радиус r основания конуса равен:
r = Lsin(α/2) = L√(1 - (L²/4R²).
Тогда S = πrL = πL√(1 - (L²/4R²)L = πL²√(1 - (L²/4R²).
2) Зависимость площади боковой поверхности S от угла α при вершине конуса в его осевом сечении.
Пусть основание конуса ниже центра шара.
Угол φ между радиусами R шара и основания r конуса равен:
φ = 90° - 2(α/2) = 90° - α.
r = Rcosφ = Rcos(90 - α) = Rsin α.
Образующая L равна:
L = r/sin (α/2) = Rsin α/sin(α/2) = R*2sin(α/2)cos(α/2)/sin(α/2) = 2Rcos(α/2).
Тогда S = πrL = πRsin α2Rcos(α/2) = 2πR²sin α*cos(α/2).
3) Зависимость площади боковой поверхности S от угла B при основании конуса.
Аналогично с пунктом 2) S = 2πR²sin 2β*sinβ.
Р=3+4+5=12
S=1/2*4*3=6 кв.ед.