Объяснение:
Животные у которых явно видны при
Млекопитающие:
-Многие животные делают запасы на зиму,пряча их под землёй,в дуплах,под камнями и т.д. В суровые зимы ,когда пищи достаточно мало это их от голодной смерти.Многие запасают эти же запасы "в себе"(накапливают жир)
-Многие животные научились линять по сезонно(тот же самый пример -заяц беляк)
-У многих животных густой мех с двойным подшёрстком,который животных от суровых зим
-Многие впадают в спячку
-Запас
Птицы:
-запасы на зиму
-сезонные миграции и перелёты
-отдельные при типа у клеста специальный клюв)
Рептилии и земноводные:
-многие рептилии умеют задерживать беременность
-меньшая зависимость от солнца нежели у более южных представителей(в биологию далеко не буду вникать,но если запишите это,припишите,что такой обладают не все(рептилии крайне зависимы от солнца .. из этой группы в западно-сибирской тайге обитает только гадюка и ещё пару земноводных,которым удалось при к такому климату,но это уже биология))
-умение впадать в оцепенение
Растения:
-крайне много тенелюбивых растений(из-за господствующих голосеменных,которые закрывают своими кронами всё небо)
-из-за голосемянных почва достаточно кислотна,поэтому при к кислотности
-многие растения вступают в симбиоз с др. организмами,например с грибами
-у древесных растений-это по сезонный опад листьев
ну,из основных думаю всё.
будут вопросы,пиши
Удачи!
Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
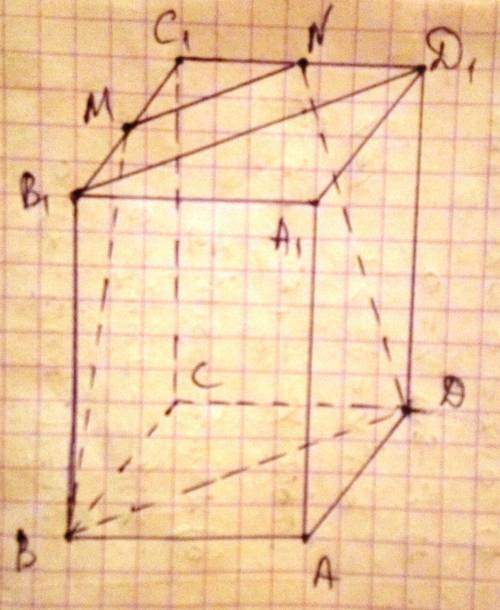
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.
L2 = 2R*sin α.
Здесь α - это центральный угол первой дуги.
sin α = 2sin(α/2)*cos(α/2).
Первая хорда L1 равна:
L1 = 2R*sin (α/2).
Находим значения синуса и косинуса угла (α/2).
sin (α/2) = (L1/2)/R = (6/2)/5 = 3/5.
cos (α/2) = √(1 - (3/5)²) = √(1 - (9/25)) = √(16/25) = 4/5.
Тогда sinα = 2/(3/5)*(4/5) = 24/25.
Теперь определяем длину искомой хорды.
L2 = 2R*sin α = 2*5*(24/25) = 48/5 = 9(3/5) = 9,6.