3,9,8,7,1
Вроде так, но это не точно
Два треугольника, которые можно совместить наложением, называются равными.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
4)
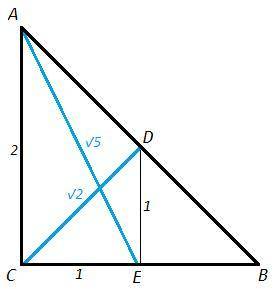
CE =BC/2 =AC/2
CE:AC:AE = 1:2:√5 (по теореме Пифагора)
DE =AC/2 (средняя линия в ABC)
CE:DE:CD = 1:1:√2
AE:CD = √5:√2 <=> AE^2:CD^2 = 5:2
5)
В равнобедренном треугольнике высота, медиана и биссектриса к основанию совпадают.
Медианы треугольника делятся в отношении 2:1 от вершины.
BH - медиана и высота, BM:MH=2:1, MH=16, BH=MH*3=48.
Биссектриса делит сторону треугольника в отношении прилежащих сторон.
DH=18, BD=48-18=30
BH - биссектриса и высота, AB:AH=BD:DH =30:18=5:3
BAH - египетский треугольник, AH=3x, BH=4x, AB=5x
P(ABC)=16x =BH*4=192
7)
AD - биссектриса, BM - медиана. Точка D на медиане, BD=5, MD=2.
Биссектриса делит сторону треугольника в отношении прилежащих сторон.
AB:AM =BD:MD =5:2
AM=AC/2 => AB:AC =5:4
ABC - египетский треугольник, BC=3x, AC=4x, AB=5x
BM=√(CM^2+BC^2) =x√13
AB=BM*5/√13 =35/√13 ~9,7
Р = 4,8 * 3 = 14,4 (см)
ответ: 14,4 см - периметр Δ.
2) В равнобедренном Δ боковые стороны равны
7,3 + 7,3 = 14,6 (см) - сумма двух боковых сторон
22,3 - 14,6 = 7,7 (см)
ответ: 7,7 см - основание Δ
3) Углы при основании равнобедренного треугольника равны.
⇒ ∠А = ∠С.
Сумма углов треугольника = 180°=
⇒∠А = ∠С = (180° - 74°) : 2 = 106° : 2 = 54°
Биссектриса делит угол пополам,
⇒ ∠ВАD = ∠САD = 54° : 2 = 27°
ответ: ∠САD = 27°
4) Медиана делит противоположную сторону пополам
⇒ DС = ВD = 12 (см);
ВС= 12+12 = 24 (см)
АВ = ВС (по условию)
АВ = 24см
AB + DC = 24 + 24 = 48 (cм) - сумма двух сторон
А дальше не решается, задача написана не до конца.