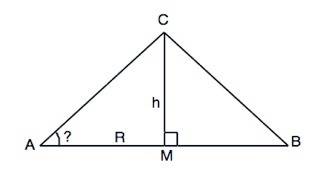
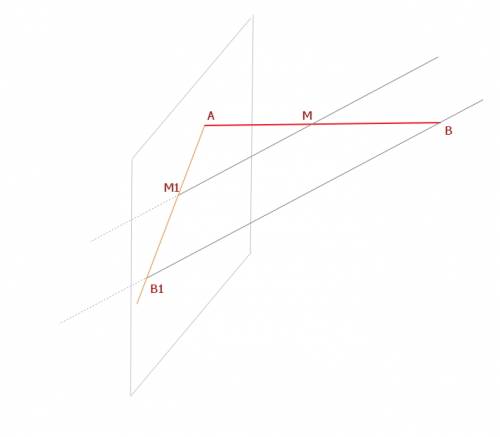
На рисунке в приложении ∆ АСВ - осевое сечение конуса, АВ - диаметр, СМ - высота конуса.
Площадь основания конуса - площадь круга.
S(кр)=πR²
Площадь осевого сечения - площадь треугольника АСВ.
S(ACB)=СН•АВ:2=h•R
По условию 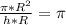 .
.
Выразим h из этого уравнения.
h=πR²:πR , 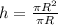 после сокращения получаем h=R
после сокращения получаем h=R
В прямоугольном ∆ АМС катеты АМ=СМ. Этот треугольник равнобедренный. Острые углы равнобедренного прямоугольного треугольника равны 45°.
Следовательно, искомый угол 45°
Во-первых, так как треугольник ABC – равносторонний,
то ∠ABD = 60°.
Во-вторых, так как треугольник BDE – равносторонний,
то ∠DBE = 60°.
Тогда в треугольниках ABD и CBE:
AB = BC, BD = BE, ∠ABD = ∠DBE = 60°.
По первому признаку равенства треугольников
ΔABD = ΔCBE.
Следовательно, AD = CE.
Объяснение: в равностороннем треугольнике все углы и стороны равны.
все проверено в онлайн мектепе и все правильно! 10/10
Также если вы дошли до 8 задания то ответ будет:
Рабс=24см. АС=8см. АД=85см.
И 9 задание:
21 см.
Все правильно :)
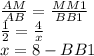
S=1/2*2R*H=RH -- площадь осевого сечения
πR²:RH=π, R:H=1, R=H
tgβ=H/R, tgβ=1, β=45° -- искомый угол