Объяснение:
4. Используем одно из свойств прямоугольных треугольников: если катет прямоугольного треуг-ка равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°. В нашем случае КН=1/2ТН, значит, <KTH=30°.Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, найдем угол ТНК:
<THK=90-<KTH=90-30=60°.
5. Используем один из признаков равенства прямоугольных треугольников: если гипотенуза и острый угол одного прямоугольного треуг-ка соответственно равны гипотенузе и острому углу другого, то такие треуг-ки равны. В нашем случае AD - общая гипотенуза, а углы BAD и CAD равны по условию, т.к. DA - биссектриса. Треугольники ABD и ACD равны. Равны и их катеты АВ и АС.
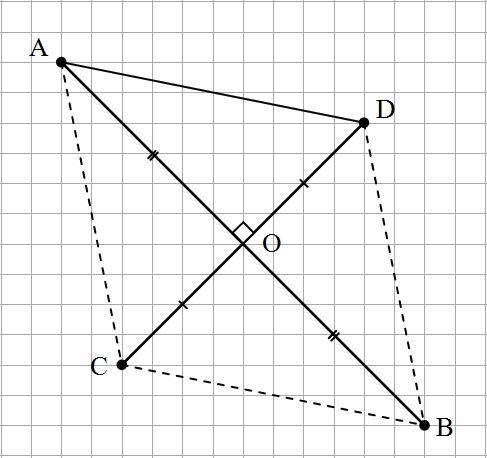
1). См. рис.1
По условию, т.О - середина отрезков АВ и СD.
Кроме того, AB⊥CD.
Четырехугольник, в котором диагонали пересекаются под прямым углом и делятся точкой пересечения пополам, является ромбом.
Следовательно, AD = DB = BC = CA = 17 (см)
В ΔАОD и ΔСОB:
АО = ОВ; СО = ОD; ∠АОD = ∠COB = 90°
Следовательно, прямоугольные треугольники ΔАОD и ΔСОB равны по двум катетам.
---------------------------------
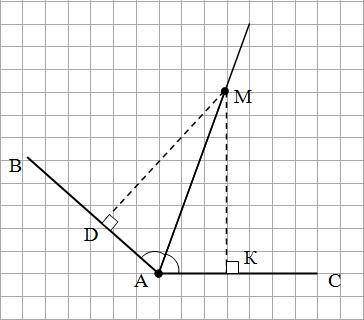
2). См. рис.2
В ΔADM и ΔАКМ:
∠ADM = ∠AKM = 90°
∠DAM = ∠KAM = 70° (АМ - биссектриса ∠ВАС)
Тогда:
∠DMA = ∠KMA = 180 - (90 + 70) = 20°
Следовательно, прямоугольные треугольники ΔADM и ΔАКМ равны по общей гипотенузе и острому углу.
--------------------------------
3). В ΔАВЕ и ΔDCE:
∠ABE = ∠DCE = 90°
∠BEA = ∠CED, как вертикальные
Тогда:
∠ВАЕ = ∠СDE = 20°
и ∠BEA = ∠CED = 180 - (90 + 20) = 70°
Так как ∠ВАЕ = ∠СDE = 20° и АВ = СD, то:
ΔABE = ΔDCE по катету и прилежащему острому углу.
Величина угла ∠АЕD:
∠АЕD = 180 - 70 = 110°
В ΔАЕD:
AE = ED, как гипотенузы в равных треугольниках.
Следовательно, ΔАЕD - равнобедренный и:
∠EAD = ∠EDA = (180 - 110) : 2 = 35°
В ΔABD и ΔACD:
∠BAD = ∠CDA = 20 + 35 = 55°
и АВ = CD
Тогда:
ΔABD = ΔACD по катету и прилежащему острому углу.