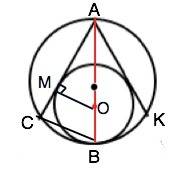
Обозначим хорды АС и АК. Они - касательные, проведенные к меньшей окружности.
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
⇒. ∠САВ=∠КАВ=60°:2=30°
Проведем СВ и КВ.
∠АСВ=∠АКВ=90° - опираются на диаметр АВ.
∆ АСВ=∆ АКВ - по гипотенузе и острому углу
⇒ АС=АК,
Проведем радиус ОМ в точку касания окружности с АС. Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒
∠АМО=90°
ОМ=r и противолежит углу 30°. ⇒ гипотенуза ОА=2r.
Тогда АВ=3r ⇒
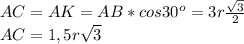
Обозначим хорды АС и АК. Они - касательные, проведенные к меньшей окружности.
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
⇒. ∠САВ=∠КАВ=60°:2=30°
Проведем СВ и КВ.
∠АСВ=∠АКВ=90° - опираются на диаметр АВ.
∆ АСВ=∆ АКВ - по гипотенузе и острому углу
⇒ АС=АК,
Проведем радиус ОМ в точку касания окружности с АС. Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒
∠АМО=90°
ОМ=r и противолежит углу 30°. ⇒ гипотенуза ОА=2r.
Тогда АВ=3r ⇒
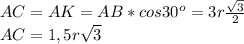

∆АВС- прямоугольный
АС=7см
<А=45°
Найти: АВ-?
Решение:
1) так как сумма двух острых углов в прямоугольном треугольнике равна 90°, то угол <В=45°
Следовательно треугольника равнобедренный
2)Тогда его катеты равны 7 см, а так как гипотенузу можно найти по теореме Пифагора ,
ответ: