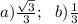
Объяснение:
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
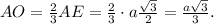
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
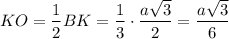
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.
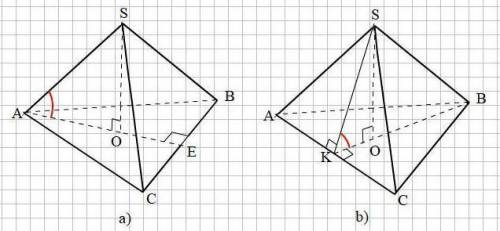
H=6
Найти h(бок)
Решение:так как треугольник равнобедренный,все бока равны.Допустим,
у нас BD=6(высота).ЕМ-высота боковой стороны.Поэтому,ЕМ разделяет треугольник на 4 равные части,то есть BD/4=6:4=1,5.ЕМ разделяет BD на две части ,поэтому BD/2=6:2=3.Последовательно,нам нужно 3:1,5=2
ответ:2.