Трегуольники abc и a1b1c1 подобны причем сторонам ab и bc соответствуют стороны a1b1 и b1c1. найдите неизвестные стороны этих треугогльников. ab=12см a1b1=6см a1c1=9см b1c1=8см

👇

Ответ:

yuliko13

06.07.2021

Отношение сходственных сторон треугольников
АВ:А1В1=12:6=2 ⇒ коэффициент подобия k=2
Тогда остальные стороны треугольника АВС равны
АС=9•2=18 см
ВС=8•2=16 см

4,8(15 оценок)

Открыть все ответы

Ответ:

123456471

06.07.2021

1

5-9

Геометрия

Высота трапеции равна 7 см,а одно из оснований в 5 раз больше другого.найдите основания трапеции,если ее площадь равна 84 кв.см

1

Попроси больше объяснений

Следить  Отметить нарушениеот KatarinaKim 13.05.2012

ответы и объяснения

Hrisula

Ведущий Модератор2012-05-13T18:33:20+04:00

Примем меньшее основание за х.

Тогда большее будет 5х

Площадь трапеции равна произведению полусуммы оснований на ее высоту.

Площадь и высота даны в условии

Полусумма

84:7=12 см

Полусумма оснований равна

(5Х+х):2=12

3х=12

х=4 см - меньшее основание.

4*5=20см - большее основание.

4,5(29 оценок)

Ответ:

hide2

06.07.2021

ответ:

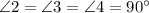1) $\angle 2 = \angle 3 =\angle 4 = 90^{\circ}$ ; 2) Величина острого (наименьшего) угла.

Объяснение:

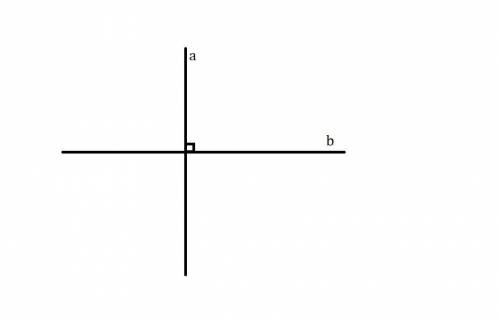
1) Начертим две пересекающие прямые. Обозначим их буквами и

При их пересечении, образовался угол в 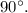$90^{\circ}.$

Пусть 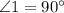$\angle 1 = 90^{\circ}$

Вертикальные углы равны.

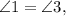$\angle1=\angle3,$ как вертикальные.

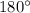Сумма смежных углов равна $180^{\circ}$ .

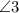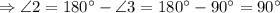
$\angle 2$ и $\angle 3$ - смежные $\Rightarrow \angle 2 = 180^{\circ} - \angle 3 = 180^{\circ} - 90^{\circ} = 90^{\circ}$

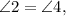$\angle 2 = \angle 4,$ как вертикальные.

2) Угол между двумя пересекающимися прямыми - это величина наименьшего угла между двумя пересекающимися прямыми.

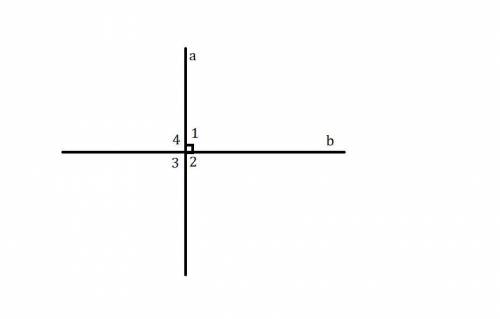
Обозначим две пересекающиеся прямые буквами и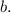

При пересечении произвольных прямых, образуются 4 угла: 2 равных тупых угла и 2 равных острых угла (они равны, как вертикальные).

В данном случае наименьший угол - это величина острого угла, так как величина острого угла меньше тупого.

=============================================================

Но если прямые перпендикулярные (прямые, при пересечении которых образуются 4 прямых угла), то наименьший угол - это величина прямого. Но в данной задаче этого не уточняется, поэтому верный ответ - величина острого угла.